Predecir y verificar, estrategia para resolver problemas
https://eduteka.net/articulos/Algebra1
PREDECIR Y VERIFICAR
UNA ESTRATEGIA VIABLE PARA RESOLVER PROBLEMAS
Por Lou Feicht
Las Hojas de Cálculo ayudan a que los estudiantes de manera intuitiva logren una mejor comprensión del álgebra.
Al utilizar una hoja de cálculo, los estudiantes se integran con su lenguaje. La hoja de cálculo puede convertirse en su puente para penetrar en el mundo de las matemáticas: se les abre la oportunidad de usar este método intuitivo para resolver problemas mediante la construcción de tablas, porque los programas las generan en forma muy sencilla. Así, una hoja de cálculo resulta ser una herramienta poderosa porque permite a los estudiantes apoyarse en su intuición y aplicar una estrategia de predecir y verificar. Mis estudiantes siempre han resuelto a través de la predicción y verificación problemas como los que se presentan en este artículo, a pesar de mi esfuerzo por ofrecer otros métodos. Problemas que pueden abordarse mediante la búsqueda de patrones, con predicción y verificación o con creación de tablas, se ajustan con naturalidad al ámbito de las Hojas de Cálculo informáticas. De hecho, cualquier problema que requiera hallar un valor numérico para el cual dos cantidades sean iguales se presta para utilizar la estrategia de la Hoja de Cálculo según la cual “no se debe gastar tanto tiempo adivinando y más bien deben verificarse los valores posibles.”
La gran ventaja de utilizar un computador es que se puede verificar cada una de las posibilidades relevantes para cada respuesta. La solución de problemas con Hojas de Cálculo obliga a los estudiantes a dividir los problemas en partes más pequeñas.
PROBLEMAS DE MODELACIÓN MEDIANTE EL USO DE HOJAS DE CÁLCULO
El primer ejemplo es un típico problema algebraico:
Se pagaron 166 entradas a un partido. El precio de las boletas era $2.10 para adultos y $0.75 para niños.
Se recibió la suma de $293.25. ¿Cuántos adultos y cuántos niños asistieron?
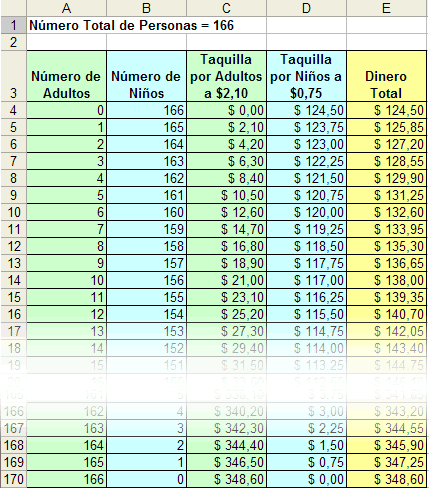
La Figura 1 muestra una manera de plantear este problema utilizando una Hoja de Cálculo [1], mientras que en la Figura 2 aparece la Hoja de Cálculo y las fórmulas subyacentes [2]. La mayoría de los estudiantes aprenderán a crear una tabla. El número de adultos que asistió al partido está en un rango entre 0 y 166, lo que sabemos como resultado del planteamiento algebráico tradicional del problema.
 |
|
Figura 1. Un enfoque que utiliza la Hoja de Cálculo para resolver el problema de las boletas de entrada a un evento. |
 |
|
Figura 2. Hoja de cálculo en la que se revela una de las maneras de configurar las fórmulas [2]. |
 |
| Figura 3. El problema de las monedas se plantea de forma similar al problema de las boletas. |
 |
|
Figura 4. El problema de la temperatura formulado para estudiantes más jóvenes. |
 |
|
Figura 5. El primer intento de estudiantes de 6º y 7º para resolver el problema de la temperatura. |
 |
|
Figura 6. Fórmulas para temperatura en la hoja de cálculo después de que los estudiantes reconocieron cómo utilizar las variables. |
|
|
|
Figura 7. Hoja de cálculo de temperaturas en la que se muestra la solución correcta.
|
|
|
Figura 1. Un enfoque que utiliza la Hoja de Cálculo para resolver el problema de las boletas de entrada a un evento. |
|
|
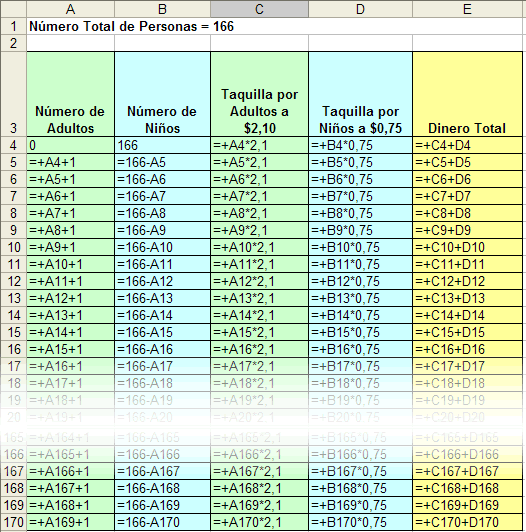Figura 2. Hoja de cálculo en la que se revela una de las maneras de configurar las fórmulas [2]. |
Sin embargo, cuando se utiliza la hoja de cálculo para resolver este problema, surgen diferencias sutiles pero importantes. En la columna correspondiente al número de adultos que asistieron al partido, se enumeran todas las posibilidades o, en esencia, cada uno de los valores posibles del dominio para la variable independiente. El número de adultos podría ser un número entero entre 0 y 166. No obstante, aún no se ha incorporado el nivel de abstracción que resultaría al introducir una variable x en el problema.
Para formular las columnas correspondientes al número de niños se infiere que, como hubo 166 personas en el partido, el número de niños que asistieron debería ser 166 menos el número de adultos. Por ejemplo, si asistieron 3 adultos, entonces debieron haber asistido 163 niños (166 – 3). Si los estudiantes conocen bien las Hojas de Cálculo, podrían anticipar la fórmula correcta que deberían utilizar para calcular el número de niños. De lo contrario, este es un excelente ejemplo para desarrollar el proceso de la fórmula. Se utiliza la notación “=166–A5” para indicarle a la Hoja de Cálculo que deberá restar la cantidad que contenga, almacene o represente la celda A5. Además, al desarrollar el concepto de variable se permite a los estudiantes apreciar en la misma página tanto todas las instancias específicas como la generalización.
A continuación se configurará la columna para el dinero que se obtendría por concepto del pago de los adultos, correspondiente a $2.10 por cada boleta. Se utiliza la hoja de cálculo para desarrollar fórmulas como “=A4*2.10”. En forma parecida, el dinero correspondiente al número de niños que asisten se representará por medio de una fórmula como “=B4*0.75”. La última columna, correspondiente a todo el dinero recaudado, tendría la fórmula “=C4+D4”.
En este momento ya se puede encontrar una solución a la pregunta original. Se busca en la columna titulada “Dinero Total”, un valor de $293.25, para ver cuántos adultos y cuántos niños asistieron. La respuesta es 125 adultos y 41 niños.
EL PROBLEMA DE LAS MONEDAS
Otro ejemplo muy común que aparece en la misma sección de un texto de álgebra es el problema de las monedas.
En una mesa hay 20 monedas de veinticinco y de diez centavos, cuyo valor combinado es de $3.05. ¿Cuántas monedas de cada valor hay?
|
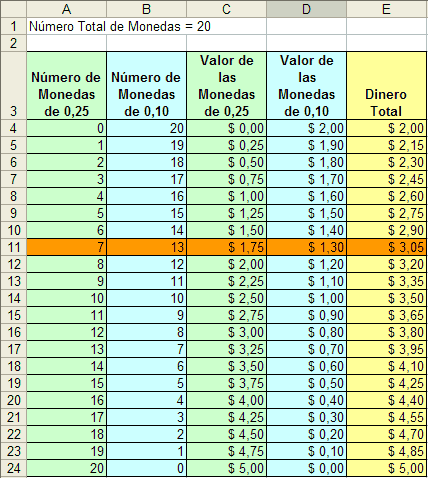| Figura 3. El problema de las monedas se plantea de forma similar al problema de las boletas. |
Este problema sigue el mismo esquema del problema de las boletas, utilizando de la misma forma una Hoja de Cálculo. (Figura 3). Es razonable asumir que más estudiantes podrían resolver el problema de las monedas que el problema de las boletas utilizando únicamente papel y lápiz porque tienen más posibilidades de predecir y verificar con éxito, pues están más familiarizados con el dinero que con las boletas. Utilizar una Hoja de Cálculo involucra una variación de la estrategia de adivinación y verificación; sencillamente se predicen y verifican todas las posibilidades y en el proceso se comienzan a desarrollar las habilidades de lenguaje y de razonamiento abstracto necesarias para comprender el álgebra.
EL PROBLEMA DE LA TEMPERATURA
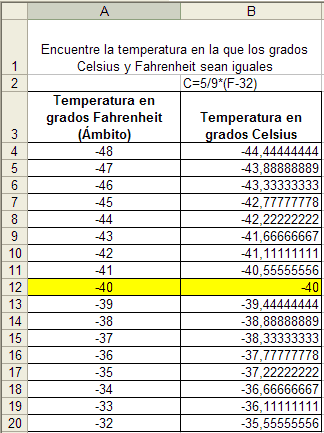
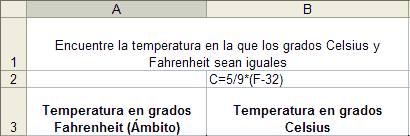
Encuentre una temperatura en la que los grados Celsius y Fahrenheit sean iguales. A los estudiantes de séptimo grado se les dieron las fórmulas para convertir los grados Celsius a grados Fahrenheit y viceversa, y se les pidió que configurarán una Hoja de Cálculo parecida a la de la Figura 4, utilizando la fórmula para grados Celsius [C=5/9(F–32)] y así hallar la temperatura en grados Celsius que equivaliera a la temperatura en grados Fahrenheit (debe advertirse que estos estudiantes ya tenían experiencia de trabajo con Hojas de Cálculo y fórmulas). Cuando se escogió el ámbito del problema y la forma de rotular las columnas, en esencia se estaba resolviendo el problema. Cuando los estudiantes adquieran suficiente experiencia serán capaces de escoger sus propias variables independientes y dependientes, títulos de columnas y fórmulas.
|
|
Figura 4. El problema de la temperatura formulado para estudiantes más jóvenes. |
También te podría interesar
Estándares tanto para alfabetismo en medios como para hablar y escuchar
Ver artículoEl Pensamiento Crítico, más allá del Procesador de Texto
Ver artículoCiudadanía Digital
Ver artículo
|
|
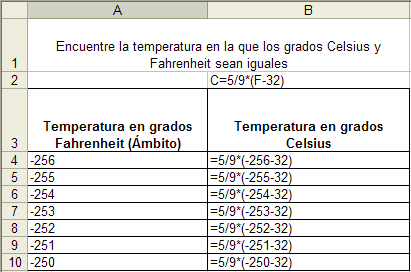
Figura 5. El primer intento de estudiantes de 6º y 7º para resolver el problema de la temperatura. |
Aunque se digitó la fórmula para grados Celsius, no todos los estudiantes supieron de inmediato cuál sería el paso siguiente. La mayoría de los estudiantes de sexto y séptimo grado comenzaron por digitar una fórmula en la celda B4 parecida a “=5/9*(–256–32)” (Figura 5). Algunos estudiantes continuaron digitando esta clase de fórmula durante el resto de la clase y yo permití que lo hicieran. ¡Ellos revisaban¡ cada una de las fórmulas para los grados Celsius utilizando la Hoja de Cálculo como calculadora y digitando bastante! Nótese que resolver el problema de esta manera no ofrece ventajas sobre el uso de una calculadora o el uso de lápiz y papel pero evidencia el inicio de algún nivel de abstracción, puesto que los estudiantes demuestran destreza para aplicar la fórmula y reemplazar en esta la variable “F” con un número.
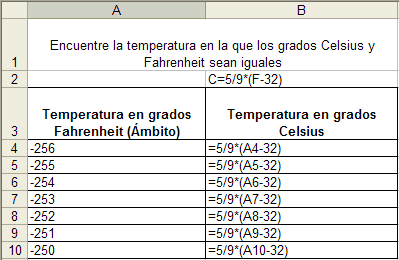
Sin embargo, la mayoría de los estudiantes se cansaron de esto rápidamente y buscaron una solución más sencilla. Después de digitar cerca de 10 fórmulas específicas, la mayoría de ellos comenzó a buscar formas de aprovechar las ventajas de la Hoja de Cálculo, pues ya tenían experiencia tanto en el uso de fórmulas como en el de la función de “Relleno Hacia Abajo”, en vez de digitar en cada celda. Estaban buscando una forma para generalizar y utilizar una variable y al observar el patrón creado en la Figura 5 descubrieron cómo el único número que cambiaba (variaba) en la columna B era la temperatura en grados Fahrenheit. Luego reconocieron que cada uno de estos números variables aparecía en la columna A y rápidamente reemplazaron sus números específicos con una fórmula más general, rellenaron las celdas hacia abajo (Figura 6) y hallaron así la solución de –40° (Figura 7).
|
|
Figura 6. Fórmulas para temperatura en la hoja de cálculo después de que los estudiantes reconocieron cómo utilizar las variables. |
|
|
|
Figura 7. Hoja de cálculo de temperaturas en la que se muestra la solución correcta.
|
CERRAR LA BRECHA ENTRE LO ESPECÍFICO Y LO GENERAL
Utilizando el primer problema como ejemplo, la diferencia con un enfoque tradicional es que los 167 casos, entre 0 y 166 adultos, tienen sus propias ecuaciones únicas. Se utilizan ecuaciones, variables y fórmulas pero no se ha dado el salto inmediatamente a utilizar una ecuación única para representar todo el problema. Los estudiantes sin formación en álgebra podrán formular este problema y resolverlo; podrán ver cada una de las posibles situaciones en la Hoja de Cálculo, de manera que el nivel de abstracción se ha reducido inicialmente de una ecuación única, como en el enfoque tradicional, a establecer los cimientos del razonamiento algebraico. Los estudiantes que pudieron formular el problema utilizando el enfoque algebraico tradicional sin resolver la ecuación correctamente, podrán ahora obtener la solución acertada.
Ya podemos quitarle las rueditas de entrenamiento al aprendizaje y darle a los estudiantes un modelo más general del problema. Aunque cada caso tiene su propia fórmula en la Hoja de Cálculo, el breve salto hacia la formulación de una ecuación que represente todo el problema utiliza las tres últimas columnas “(A129*2.10 + B129*.75=293.25)”. La propiedad de sustitución de iguales puede utilizarse para reemplazar B129; los estudiantes entienden intuitivamente esto, pues ven que la celda B129 contiene 166–A129. Nuestra ecuación se convertiría en “A129*2.10 + (166–A129)*.75= 293.25”, que es precisamente dónde podríamos haber comenzado el problema sin una hoja de cálculo, usando únicamente una notación diferente “(2.10x +75(166–x)=293.25)”.
El uso de la hoja de cálculo es de gran utilidad para que los maestros ayuden a los estudiantes a alcanzar el nivel final de abstracción. La evidencia sugiere que los estudiantes sin formación en álgebra conservarán la destreza para resolver este tipo de problemas aún con lápiz y papel, usando el lenguaje de la hoja de cálculo (Sutherland & Rojano, 1993) [3].
NOTAS DEL EDITOR:
[1] Un archivo de Excel 2000 con el ejemplo utilizado en este artículo se puede descargar de http://www.eduteka.org/pdfdir/Algebra1.xls
[2] Para Ver las fórmulas subyacentes en una Hoja de Cálculo se debe elegir “Opciones” del Menú “Herramientas”. En la ventana que se abre, seleccionar la etiqueta “Ver” y en la sección “Opciones de Ventana” seleccionar “Fórmulas”. Las anteriores instrucciones se aplican a Microsoft Excel 2000.
[3] Sutherland, R., & Rojano, T. (1993). Una aproximación a la Hoja de Cálculo para resolver problemas algebraicos. Journal of Mathematical Behaivior, 12, 353-383. http://www.bris.ac.uk/Depts/Education/ros.htm
CRÉDITOS:
Traducción al español realizada por EDUTEKA del artículo original “Guess and Check” escrito por Louis Feicht y publicado en el Número 5 del Volumen 27 de la revista Learning & Leading with Technology (http://www.iste.org).
Louis Feicht 
tiene una experiencia de 12 años en la enseñanza de matemáticas e informática. Trabaja como especialista en tecnología y promotor de sitios de Internet en Silverton, Oregon. También diseña aplicaciones dinámicas en la Red.
Margaret L. Niess 
es editora del área de matemáticas de Learning & Leading with Technology, enseña en Oregon State University (Universidad Estatal de Oregon). En 1993, recibió el Premio Honorífico de Excelencia al Profesorado otorgado por la OSU’s Burlington Resources Foundation por sus logros en la Enseñanza e Investigación.
Publicación de este documento en EDUTEKA: Noviembre 01 de 2003.
Última modificación de este documento: Noviembre 01 de 2003.
