
Entrevista con Bert Waits
https://eduteka.net/articulos/Handhelds1
ENTREVISTA CON BERT WAITS
COMPUTADORES DE BOLSILLO: INGREDIENTE ESENCIAL
EN LA ENSEÑANZA Y EL APRENDIZAJE DE MATEMÁTICAS
Por Terese Herrera
El nombre de Bert Waits [1] estará siempre vinculado con la obra “Nuevos Horizontes para la Educación en Matemáticas y Ciencias” [2]. Él y Frank Demana, profesores de matemáticas de la Universidad Estatal de Ohio, Estados Unidos, estuvieron entre los primeros que se dieron cuenta de que la Tecnología inevitablemente impactaría el currículo de matemáticas y en qué forma podría mejorar la instrucción en el aula de clase.
En conjunto, escribieron libros de texto en los que consideraban la tecnología como herramienta básica en la solución de problemas y la comprensión de las matemáticas, en lugar de tratarla como elemento de segundo orden. En 1988, fundaron T3 (Maestros que Enseñan con Tecnología) [3], que comenzó como un sitio de entrenamiento local en el uso de calculadoras gráficas y se convirtió en el programa de capacitación profesional más grande del mundo, enfocado a la tecnología del computador de bolsillo en el aula de clase. Juntos y por separado, Waits y Demana han sido conferencistas en numerosos eventos nacionales e internacionales. En 1997, ambos recibieron el premio “Glen Gilbert” del Consejo Nacional de Supervisores de Matemáticas (NCSM), por su sigla en inglés. [4].
Actualmente, Waits es profesor emérito de matemáticas de la Universidad Estatal de Ohio, miembro de la Junta Directiva del Consejo Nacional de Profesores de Matemáticas y consultor de la firma Texas Instruments Inc. Es autor de libros de texto para la editorial Wesley / Prentice Hall; pero más allá de todos esos títulos profesionales, es líder reconocido en las líneas de avanzada del progreso y la excelencia en la enseñanza de matemáticas.
¿En qué forma cree usted que cambiará el contenido de las matemáticas escolares cuando se integre la tecnología a la enseñanza en el aula de clase? Muy positivamente, creo yo. Este es el panorama que estoy tratando de mostrar. El contenido matemático que enseñamos ha ido evolucionando en el tiempo para servir a la sociedad. Los matemáticos han utilizado siempre las herramientas que han tenido disponibles en su época. Los logaritmos, por ejemplo, se inventaron para ayudar en los cálculos aritméticos y se convirtieron en una herramienta para calcular. Si las calculadoras hubieran estado disponibles con anterioridad, científicos y educadores las hubieran utilizado en razón de que son herramientas mejores.
El cómputo matemático (incluyendo los cálculos aritméticos y la manipulación de símbolos en álgebra y en cálculo) están profundamente influenciados por la tecnología actual. Sin embargo, todavía hay quienes piensan que el currículo debe mantenerse sin alteraciones, ignorando los cambios que ha traído la tecnología, y que se siga enseñando como se ha venido haciendo desde hace 50 o 100 años. Esto es ridículo. Es como practicar medicina sin hacer uso de los nuevos avances en las técnicas y los medicamentos.
No todo el currículo de matemáticas tiene que cambiar como respuesta a la tecnología. Además de lo que tiene que ver puramente con el cómputo, están las matemáticas que se basan en razonamiento, comprensión de conceptos, teoremas y pruebas, aplicaciones y solución de problemas. Si el estudiante hace uso de la tecnología tendrá más tiempo para enriquecer su aprendizaje matemático.
La tecnología incluso ha afectado de manera sorprendente a la matemática pura; abriendo camino para el estudio de nuevos campos de esta, como en el caso del trabajo de Mendlebrot con la geometría de Fractales [5].
¿Qué efecto tendría la tecnología en el cómputo?
La historia nos demuestra que cualquier contenido matemático que tenga que ver con el cómputo, va a cambiar por efecto de la tecnología. La lección más reciente de la historia tiene que ver con los efectos de la calculadora científica sobre el tipo de cómputo que enseñé entre 1961 y 1976. En muy pocos años, la calculadora científica convirtió en obsoletos algunos de los contenidos matemáticos que yo enseñaba en la Universidad. No entender por que pasó
lo que pasó es una locura. Lo que sucedió simplemente fue que la calculadora científica era una herramienta mejor, una mejor manera para calcular.
La misma situación se va a presentar muy pronto con un cuerpo aún mayor de la matemática tradicional. Los “Computer Algebra Systems” (CAS, por su sigla en inglés) (Sistemas Algebraicos para Computador) cambiarán radicalmente, la forma en que ahora conocemos los contenidos del álgebra y el cálculo [6]. Nos encontramos en la fase inicial de ese cambio. En 20 o 25 años, muchas de las manipulaciones que enseñamos hoy con lápiz y papel, serán vistas por la mayoría de las personas tan obsoletas como la regla de cálculo.
Actualmente muchas personas están preocupadas por la eliminación de métodos que tradicionalmente se han utilizado para enseñar matemáticas. ¿Qué les diría usted?
Si mirara nuevamente las notas de las conferencias y los libros de texto que yo usaba en los años 60, podría probarle que al menos el 25% de mi curso universitario de álgebra de ese entonces, ha desaparecido por causa de la calculadora científica. Mire, nadie es más pobre porque ya no enseñamos a los estudiantes a extraer a mano las raíces cuadradas. Es inevitable que muchas de las técnicas de lápiz y papel que se enseñan hoy en día, simplemente van a desaparecer, y nadie se va a perjudicar por esto.
Déjeme hacer una aclaración, algunos educadores sostienen que un tópico como factorización va a volverse obsoleto a causa de la tecnología. Nada podría estar más lejos de la verdad; me siento molesto cuando oigo ese tipo de cosas. Los maestros tienen que entender que la factorización es parte Fundamental del Teorema del Álgebra. El concepto de factorización, siempre será muy importante. Pero las herramientas que utilizamos para factorizar van a cambiar. La tecnología es una nueva herramienta que puede utilizarse para factorizar, además de hacerlo mentalmente o con lápiz y papel. La tecnología permite a los estudiantes dominar el concepto y les ofrece una comprensión más profunda. Si tenemos nuevas herramientas tecnológicas, no debemos tener miedo de usarlas. La factorización no se volverá obsoleta, pero algunos métodos utilizados para factorizar si se volverán. Esta es una distinción importante de hacer.
Usted menciona con frecuencia la necesidad de balancear...
Siendo una persona mayor y conservadora, yo creo firmemente en el balance.
Aunque abogo por el uso apropiado de la tecnología en la enseñanza y el aprendizaje de la ciencia y las matemáticas, creo también que la enseñanza (y el poner a prueba) las habilidades mentales para hacer cálculos, es hoy más importante que nunca. La tecnología ofrece una herramienta cómoda para calcular, pero debe emplearse correctamente. Por ejemplo, si un estudiante usa la calculadora para saber cual es el 14.5 % de $1.500 y la respuesta que encuentra es $21.750, el debe darse cuenta de que algo está muy mal!. Darse cuenta de esta situación proviene de la habilidad mental para calcular así como de la habilidad para estimar (la respuesta debe ser menos de 20% de 1,500, o 300 calculados mentalmente).
Creo además que existe un papel muy importante para las manipulaciones que se realizan con lápiz y papel. Por ejemplo, antes de empezar a utilizar, en la escuela Básica y Media, computadores de mano para graficar, los estudiantes deberían pasar un tiempo considerable graficando con lápiz y papel y entendiendo bien este proceso. Del mismo modo, antes de que los estudiantes hagan uso de un CAS (computer álgebra system) deben tener alguna comprensión de manipulaciones algebraicas simples hechas con lápiz y papel. Esto es bastante diferente de solicitar manipulaciones hechas en papel y lápiz durante todo el bachillerato (Media) y todo el programa de Cálculo. Por lo que repito, balance, balance y balance.
Nos parece que es su voz abogando por la tecnología, la que se escucha con mayor frecuencia. ¿Se debe esto a que los otros que la apoyan o respaldan no lo hacen abiertamente?
Lo que usted dice es cierto. Las personas que se oponen a la integración de los computadores de bolsillo [7] en la enseñanza y el aprendizaje de las matemáticas tienen sin duda buenas intenciones, pero para decirlo escuetamente están perjudicando nuestros niños. Ellos les están negando una mejor educación al no permitir que se beneficien de los avances en la enseñanza que la tecnología ha generado. Están promoviendo un currículo desbalanceado con lo que ellos consideran es la única forma en la que se debe aprender matemáticas: haciendo ejercicios interminables o realizando ejercicios durante toda la clase con lápiz y papel.
Nuevamente quiero llamar la atención sobre la necesidad de un currículo balanceado. Debemos incrementar los requerimientos para desarrollar la habilidad mental para calcular y estimar. Yo creo firmemente que las manipulaciones con lápiz y papel deben jugar un papel importante en ciertas etapas del currículo, pero también quiero que se reconozca el papel de la tecnología como uno de los ingredientes esenciales en la enseñanza y el aprendizaje de las matemáticas escolares.
¿De qué manera podríamos tender un puente que conectara el álgebra del lápiz y el papel con el álgebra de computador?
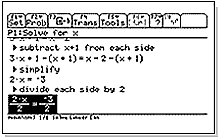
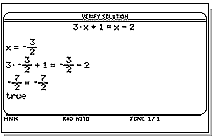
Se van a desarrollar sistemas pedagógicos de álgebra por computador que cerrarán la brecha entre la utilización de este tipo de programas de álgebra como herramienta para calcular y, el no hacer ningún uso de ellos. Por ejemplo, utilizando el software Derive de la calculadora TI-92 Plus de Texas Instruments [8], o Matemática (Wolfram Research) [9], usted puede resolver una ecuación con presionar un botón. Yo llamo esto un proceso de “caja negra”: entre la ecuación, oprima un botón, encuentre la solución. Este es un procedimiento para los estudiantes que ya dominan suficientemente los conceptos y pueden ahorrarse el “machacar números” e ir directamente a temas más importantes. ¿Verdaderamente resolví el problema? ¿Qué significa el resultado? Y otros.
En la actualidad están en desarrollo programas de álgebra pedagógicos (CAS) que requieren que el estudiante le indique a la máquina los pasos que se deben seguir para resolver una ecuación. Es el estudiante el que dirige el proceso. Constituyen un paso intermedio entre usar únicamente lápiz y papel y las soluciones de computador que llamo de “caja negra”. Al menos por ahora yo creo que esos sistemas servirán de puente para ayudar a los maestros a desarrollar estrategias para usar los programas de computador para álgebra efectivamente dentro de sus esquemas de enseñanza. La versión de Texas Instruments de este nuevo sistema, que se llama “Symbolic Math GuideA™”, se consigue gratuitamente como concepto de aplicación de la calculadora TI – 89 o la TI – 92 Plus [10].
Más atrás en la entrevista usted se refirió a la tecnología como ingrediente esencial en la enseñanza de matemáticas. ¿Podría ampliarnos la explicación?
Yo creo firmemente en los nuevos “Principios y Estándares para Matemáticas Escolares, 2000 del National Council of Teachers of Mathematics (NCTM, por su sigla en inglés) [11]. El Principio que se refiere a la Tecnología de ese documento dice: “La tecnología es esencial en la enseñanza y el aprendizaje de las Matemáticas”. Y es esencial.
La tecnología tiene que ver tanto con el contenido como con la instrucción. La tecnología puede ofrecer un adelanto pedagógico significativo para la enseñanza y el aprendizaje en ciencias y matemáticas. Como herramienta pedagógica, el computador de bolsillo con capacidad de graficar, como llamo ese dispositivo, se usa para ofrecer una aproximación representativa múltiple. Analíticamente usted puede ver un problema con lápiz y papel; o puede verlo mediante una gráfica; o puede verlo numéricamente usando tablas. Miles de maestros que utilizan los computadores de bolsillo que grafican, pueden testimoniar el poder que tiene esta forma de aproximación.
En los cursos de matemáticas para maestros en formación, debemos diseñar programas con las matemáticas de hoy, en las que hay una total integración de la tecnología y una valoración real del poder y (limitaciones) de la tecnología. El uso adecuado de la tecnología constituye parte esencial del balance del currículo. Algunos departamentos universitarios de matemáticas se resisten a realizar estos cambios en la formación de maestros. Esta es una situación muy desafortunada.
¿Qué considera usted que debe pasar antes de que la tecnología se convierta en parte integral y efectiva de la enseñanza de matemáticas?
Existen demasiados maestros con una limitada comprensión de cómo usar adecuadamente la tecnología para enseñar y cómo, la tecnología va a afectar y a cambiar el contenido de las matemáticas y las ciencias. Es necesario que los maestros tengan mayores oportunidades de desarrollo profesional que se enfoquen en estos hechos, además del compromiso decidido de hacer de la integración de la tecnología una realidad.
¿Cómo puede lograrse lo anterior?
Debemos dedicar mucho más dinero y esfuerzo en comprender la necesidad de desarrollo profesional de los maestros. Padres, legisladores y la sociedad en general, deben ponerse de acuerdo con el hecho de que es necesario un desarrollo profesional significativo y continuo y, fondear este acuerdo de manera adecuada, teniendo además en cuenta el tiempo libre que necesitan los maestros para lograrlo.
Para resumir, ¿cuál es su visión para el futuro?
Las tecnologías del computador de bolsillo y del computador personal (PC) están convergiendo. Esto comenzó a mediados de los 80 con la calculadora Casio 7000, la primera graficadora de bolsillo. Cada dos años, aproximadamente, se hace más evidente que el PC o el computador portátil y los dispositivos gráficos de bolsillo, se están fusionando. Estos dispositivos son los actuales computadores de bolsillo. Debe notar usted que yo evito utilizar la palabra “calculadora”. Podemos eliminar la palabra calculadora de nuestro vocabulario y remplazarla por “computador de bolsillo”.
Adentrémonos más en la visión de computador que tenían los educadores hace 10 años. ¿Recuerda usted el énfasis en los laboratorios de cómputo interconectados? Fueron pocas las escuelas que pudieron cumplir con esa expectativa debido a las barreras prácticas existentes. Los Laboratorios de cómputo eran costosos; era difícil llevar los estudiantes a estos; los computadores no eran portátiles. Ahora las escuelas están utilizando computadores de bolsillo que permiten que cualquier aula de clase esté completamente interconectada. Es más, los estudiantes pueden llevarse a la casa los computadores de bolsillo para explorar problemas y posteriormente hacer reportes y colaborar en clase. Los maestros pueden transmitir un conjunto de problemas, ver como cada estudiante los está resolviendo y proporcionarles retroalimentación inmediata [12].
Resumiendo mi visón del futuro: muchas de las técnicas para manipulación simbólica o para realizar cálculos en álgebra y cálculo, van a desaparecer. Como resultado de lo anterior, se tendrá un mayor tiempo disponible para enseñar verdadera matemática (comprender, razonar y resolver problemas). Además, tendremos más tiempo para hacer actividades que demuestren la utilidad y belleza de las matemáticas. Tendremos más tiempo para dedicar a las matemáticas que se han considerado inasequibles pero que ahora la tecnología permite alcanzar.
En unos pocos años, los estudiantes caminaran por las escuelas con sus computadores portátiles poco costosos, computadores de bolsillo, habilitados para trabajar en red, intercurriculares y con acceso a Internet. Podrán trabajar juntos y recibir retroalimentación oportuna del progreso que están alcanzando. El aprendizaje ya no tendrá el formato de conferencia magistral y memorización que nosotros hemos experimentado. El aula de clase verdaderamente interconectada, ofrecerá un ambiente de aprendizaje dinámico en el que todos los estudiantes puedan participar, demostrar su comprensión y dominar conceptos. El aprendizaje estará centrado en el estudiante. Es para allá que vamos, y yo, como muchos otros, estoy inmensamente entusiasmado con esto.
NOTAS DEL EDITOR:
[1] El Dr. Bert k. Waits es Profesor Emérito de Matemáticas de la Universidad Estatal de Ohaio (USA) donde actualmente es profesor visitante en la Facultad de Educación. Cofundador, internacionalmente reconocido, del programa de formación de Maestros de Matemáticas que Enseñan con Tecnología, T3 (Teachers Teaching with Technology). Autor o coautor de más de 70 publicaciones entre las que se destacan tres series de libros de texto de Precálculo y Cálculo que se utilizan en Colegios y Universidades. Por otro lado el Dr. Waits ha colaborado en el diseño de las Calculadoras Gráficas y los Computadores de Bolsillo de la firma “Texas Instruments” desde 1988. (La computadora gráfica la inventó Casio en el 85 se llamó FX – 7000). Su área de interés además de la formación de maestros, es el desarrollo de estrategias pedagógicas adecuadas para integrar el álgebra simbólica del computador de bolsillo, en la enseñanza y el aprendizaje de matemáticas en los niveles de Media y Superior.
[2] Nuevos Horizontes para la Educación en Matemáticas y Ciencias (New Horizons in Mathematics and Science Education)
[3] T3: Teachers Teaching with Technology (Maestros que Enseñan con Tecnología) proyecto de colaboración entre la comunidad educativa y Texas Instruments. Esta iniciativa tiene por objeto familiarizar al profesorado con las tecnologías que la Enseñanza Secundaria requiere, y ayudarles a que incorporen estas herramientas en su práctica cotidiana.
[4] Consejo Nacional de Supervisores de Matemáticas (NCSM, por su sigla en inglés) http://mathforum.org/ncsm/
[5] Estudio de los Fractales de Mandlebrot (se recomienda verlo con Internet Explorer 5.0 o superior) http://mathforum.org/alejandre/applet.mandlebrot.html
[6] . “Los Programas Algebraicos para Computador (CAS) consisten en programas que resuelven, calculan, simplifican, desarrollan en series y grafican expresiones del álgebra y del cálculo por medio de símbolos. Son utilizados por matemáticos profesionales y docentes. Han tenido un impacto importante en la enseñanza del cálculo. Esto constituye una relación muy estrecha entre la matemática como disciplina y la tecnología informática”. Fidel Oteiza Morra, Juan Silva Quiróz y Equipo Comenius / USACH, Chile, Enero, 2001; Computadores y Comunicaciones en el Currículo Matemático, http://www.eduteka.org/pdfdir/SilvaMatematicas.php
[7] Computador de Bolsillo es un dispositivo de mano, portátil y pequeño que permite almacenar información. Se conoce también con el nombre de PDA (Asistente Digital Personal, pos su sigla en inglés) o Handheld (Computador de Mano). Estos computadores evolucionaron a partir de las Agendas Digitales utilizadas para guardar y recuperar información (contactos, citas, notas, tareas, etc). Existen en el mercado miles de programas de todo tipo que se pueden instalar en un Computador de Bolsillo; la información se puede escribir a mano, directamente sobre la pantalla táctil de cristal líquido (LCD), utilizando un lápiz especial con punta roma o mediante un teclado externo. Los Computadores de Bolsillo se dividen en dos grandes familias de acuerdo con el sistema operativo que utilizan: Palm OS y Pocket PC. Aunque tienen una apariencia y un funcionamiento diferentes, son afines en muchos aspectos.
 |
 |
|
Palm |
PocketPC
|
 |
 |
 |
 |
|
Symbolic Math GuideA
|
|
 |
 |
|
Palm |
PocketPC
|
[8] Calculadora TI-92 Plus
 |
 |
También te podría interesar
Cómo seleccionar herramientas digitales con propósitos educativos
Ver artículoEl Principio de la tecnología para matemáticas escolares
Ver artículoLa Intregración de las Tecnologías de la Información y las Comunicaciones al Currículo Regular
Ver artículoLa Intregración de las Tecnologías de la Información y las Comunicaciones al Currículo Regular
Ver artículoLa calculadora TI-92 es un minicomputador de mano, con seis programas diferentes que tienen sus propios comandos y funciones:
-
Un programa de Álgebra y cálculo (HOME) para realizar todas las operaciones de una calculadora científica, más
-
Operaciones de Álgebra (factorización, solución de ecuaciones, ...) y cálculo (integración, derivación, ...).
-
Un programa de geometría dinámica plana (CABRI G…OM»TRE), en el que pueden construirse figuras geométricas de acuerdo con las reglas de la geometría euclidiana (puntos, segmentos, circunferencias...), y la geometría analítica (ejes de coordenadas, ecuaciones, ...).
-
Un programa de edición y graficación de funciones (Y = , GRAPH, TABLE, WINDOW).
-
Un editor de texto.
-
Un editor de programas.
-
Una hoja de cálculo.
[9] Matemática (Wolfram Research): Software de matemáticas para estudiantes, ingenieros, analistas financieros e investigadores. http://www.wolfram.com/products/
[10] Los conceptos de aplicaciones (Concept Apps) son programas gratuitos de Texas Instruments que se distribuyen por medio de una ventana personal de descarga y que pueden transferirse de un computador de bolsillo a otro. El software “Symbolic Math GuideA”. Puede descargarlo gratuitamente de la siguiente dirección: http://education.ti.com/us/product/tech/92p/apps/apps.html
 |
 |
|
Symbolic Math GuideA
|
|
[11] El Principio de la Tecnología para Matemáticas Escolares. Documento del Consejo Estadounidense de Profesores de Matemáticas (NCTM) que contiene la posición de este organismo respecto al uso de la Tecnología en la enseñanza de esta área. Los principios describen algunas características de la educación de calidad. http://www.eduteka.org/PrincipiosMath.php
[12] Ver el artículo “Probando el Navegador” en el cual se expone un ejemplo en el aula de clase. http://www.enc.org/features/focus/archive/horizons/document.shtm?input=FOC-002316-index
CRÉDITOS
Traducción al español realizada por EDUTEKA de la Entrevista original “Handheld Technology: An Essential Ingredient in Teaching and Learning Mathematics” realizada por Terese Herrera y publicada en el Sitio Web ENC (Eisenhower National Clearinghouse) http://www.enc.org/features/focus/archive/horizons/document.shtm?input=FOC-002315-index
Terese Herrera es especialista en recursos matemáticos del equipo de Recursos Instruccionales en ENC (http://www.enc.org). Lleva 15 años como profesora en niveles de Básica y Media.
Publicación de este documento en EDUTEKA: Noviembre 29 de 2003.
Última modificación de este documento: Noviembre 29 de 2003.




