
Evaluación Pisa 2003 Matemáticas
https://eduteka.net/articulos/Pisa2003Math
COMPETENCIA EN MATEMÁTICAS (OCDE / PISA)
En su edición del 26 de julio pasado, EDUTEKA publicó la traducción de algunos apartes del capítulo sobre “Competencia en Lectura” [1] del informe del año 2003 de OCDE / PISA [Programa Internacional de Evaluación de Estudiantes auspiciado por la UNESCO y la Organización para la Cooperación y el Desarrollo Económico (OCDE)]. El objetivo de la evaluación internacional que hace OCDE / PISA es establecer hasta qué punto los sistemas educativos de los países participantes (42 en 2003) están preparando a sus estudiantes de 15 años para jugar un papel constructivo como ciudadanos participes en la sociedad. Siguiendo la misma línea, EDUTEKA pone ahora a disposición de sus usuarios los elementos centrales del capítulo sobre “Competencia en Matemáticas” de este importante informe.
DEFINICIÓN DEL DOMINIO
El dominio de Competencia en Matemáticas de OCDE / PISA concierne la capacidad de los estudiantes para analizar, razonar y comunicar eficazmente sus ideas al tiempo que se plantean, formulan, resuelven e interpretan problemas matemáticos en una variedad de contextos. La evaluación de OCDE / PISA se concentra en problemas de la vida real que van más allá de las situaciones y problemas que típicamente se encuentran dentro del salón de clase. En el mundo real, las personas se enfrentan frecuentemente con situaciones en las cuales la aplicación de técnicas de razonamiento cuantitativo o espacial, así como de otras herramientas matemáticas, puede contribuir a clarificar, formular o resolver un problema. Este es el caso, por ejemplo, cuando las personas van de compras, viajan, preparan alimentos, revisan sus finanzas personales o tratan de formarse opiniones sobre cuestiones de interés político, etc.
Estas aplicaciones de las matemáticas se basan en las habilidades desarrolladas a partir de los tipos de problemas que aparecen en los libros de texto escolares y los que se plantean en los salones de clase. No obstante, las mismas demandan la capacidad adicional de emplear las herramientas en contextos menos estructurados, donde las instrucciones son menos claras y donde el estudiante debe tomar decisiones sobre cuáles conocimientos son relevantes y cómo se pueden aplicar de manera eficaz.
El nivel de competencia en matemáticas de OCDE / PISA se refiere a la medida en la que estudiantes de 15 años pueden ser considerados como ciudadanos reflexivos y bien informados además de consumidores inteligentes. En todo el mundo, las personas se enfrentan a una diversidad cada vez mayor de tareas que involucran conceptos cuantitativos, espaciales, probabilísticos, etc. Por ejemplo, los medios contienen gran cantidad de información presentada en tablas, cuadros y gráficos sobre temas como el clima, la economía, la medicina, y el deporte, para solo nombrar unos pocos. Los ciudadanos están sometidos a un bombardeo continuo de información sobre asuntos tales como “el efecto invernadero y el calentamiento global”, ”el crecimiento poblacional”, “los derrames petroleros en el mar”, “la desaparición de los bosques nativos”. Por último e igualmente importante, las personas enfrentan la necesidad de leer formularios, interpretar horarios de trenes y buses, realizar transacciones financieras, etc. La competencia matemática de OCDE / PISA se enfoca en la capacidad de los estudiantes de utilizar su conocimiento matemático para enriquecer su comprensión de temas que son importantes para ellos y promover así su capacidad de acción.
OCDE / PISA define de la siguiente manera la competencia matemática:
La competencia matemática es la capacidad de un individuo para identificar y entender el rol que juegan las matemáticas en el mundo, emitir juicios bien fundamentados y utilizar las matemáticas en formas que le permitan satisfacer sus necesidades como ciudadano constructivo, comprometido y reflexivo.
Una habilidad crucial implícita en esta noción de la competencia matemática es la capacidad de plantear, formular, resolver, e interpretar problemas empleando las matemáticas dentro de una variedad de situaciones y contextos. Estos contextos van desde los puramente matemáticos a aquellos que no presentan ninguna estructura matemática aparente (en este caso la persona debe introducir ella misma la estructura matemática). También es importante enfatizar que la definición no se refiere solamente a un nivel mínimo básico de conocimiento de las matemáticas. Al contrario, la definición atañe a la capacidad de utilizar las matemáticas en situaciones que van de lo cotidiano a lo inusual y de lo simple a lo complejo.
Ciertas actitudes y emociones relacionadas con las matemáticas como la confianza en sí mismo, la curiosidad, la noción de lo que es relevante, y el deseo de hacer o comprender cosas, no son componentes explícitos de la definición de competencia matemática, pero no obstante contribuyen de manera importante a la misma. En principio, es posible poseer competencia matemática sin tener estas actitudes y emociones. Sin embargo, en la práctica, es poco probable que esta competencia vaya a ser aprovechada y puesta en uso por una persona que carezca de confianza en sí misma, curiosidad, noción de lo relevante, y deseo de hacer y entender cosas con cierto componente matemático. Por lo tanto, es fundamental reconocer la importancia de estos factores. Aunque estas actitudes y emociones no hacen parte de la evaluación de competencia matemática de OCDE / PISA, las mismas serán tratadas en otras secciones del informe.
MARCO TEÓRICO DEL ESQUEMA MATEMÁTICO DE OCDE / PISA
La definición de competencia o “alfabetismo” matemático de OCDE/PISA es consistente con los elementos generales de la teoría de la estructura y el uso del lenguaje que surge de los más recientes estudios socio-culturales. La capacidad de leer, escribir, escuchar y hablar un lenguaje es la herramienta más importante de la sociedad humana. De hecho, cada lenguaje humano posee un diseño intrincado enlazado en formas complejas a una variedad de funciones. El que una persona sea competente en un lenguaje, implica que la persona conoce muchos de los elementos fundamentales del lenguaje y es capaz de utilizar esos elementos en pro de diversas funciones o propósitos sociales. De la misma manera, el considerar las matemáticas como un lenguaje, implica que los estudiantes deben aprender los elementos fundamentales del discurso matemático (los términos, signos, símbolos, procedimientos, habilidades, etc.) y saber aplicarlos para resolver problemas en una variedad de situaciones entendidas en términos de su función social.
Estas nociones académicas sobre la relación entre “elementos fundamentales” y “funciones” que apoyan el esquema matemático de OCDE / PISA se pueden ilustrar a través del siguiente ejemplo.
| Ejemplo Matemático 1: Alumbrado Público
El consejo municipal ha decidido poner un reflector en un pequeño parque triangular de manera que éste ilumine todo el parque. ¿Dónde debería ubicarse el reflector? |
| Ejemplo Matemático 1: Alumbrado Público
El consejo municipal ha decidido poner un reflector en un pequeño parque triangular de manera que éste ilumine todo el parque. ¿Dónde debería ubicarse el reflector? |
También te podría interesar
¿Cefalalgia? ¿Está loco el MEN?
Ver artículoLa Integración de las TIC en Competencias Ciudadanas
Ver artículoEntrevista con Bert Waits
Ver artículo¿Cefalalgia? ¿Está loco el MEN?
Ver artículoEste problema social se puede resolver siguiendo la estrategia general que aplican los matemáticos, es decir, a través de la matematización del problema. La matematización consta de cinco aspectos:
- Se parte de un problema del mundo real;
Establecer la ubicación óptima para un reflector en un parque. - Se formula el problema en términos de conceptos matemáticos;
El parque se puede representar como un triángulo, y la iluminación como un círculo con el reflector en el centro. - Gradualmente se abstrae de la realidad a través de procesos tales como hacer supuestos sobre cuáles aspectos del problema son importantes, la generalización del problema y su formalización (estos permiten transformar el problema real en un problema matemático que representa la situación en forma fehaciente);
El problema se convierte en ubicar el centro de un círculo que circunscriba el triángulo. - Se resuelve el problema matemático; y
Basándose en el hecho de que el centro de un círculo que circunscribe un triángulo yace en el punto de intersección de los bisectores perpendiculares de los lados del triángulo, construir los bisectores perpendiculares de dos de los lados del triángulo. El punto de intersección de los bisectores es el centro del círculo. - Se hace conciencia de la solución matemática en términos de la situación real.
Relacionar este hallazgo con el parque real. Reflexionar sobre la solución y reconocer, por ejemplo, que si una de las tres esquinas del parque fuera un ángulo obtuso, está solución no funcionaría, pues el reflector quedaría por fuera del parque. Reconocer que la localización y tamaño de los árboles del parque son otros factores que afectan la utilidad de la solución matemática.
Son estos procesos (representados gráficamente en el diagrama 1.1) los que caracterizan, en términos generales, cómo los matemáticos hacen matemáticas, cómo las personas utilizan las matemáticas en un sinnúmero de actividades, y cómo ciudadanos bien informados y reflexivos deben usar las matemáticas para interactuar de manera integral y competente con el mundo real.
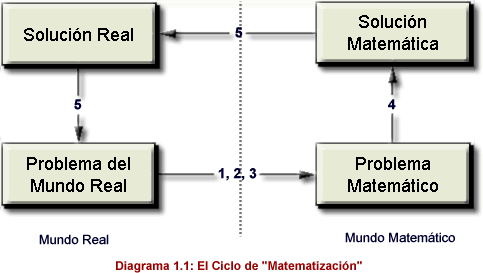
Idealmente, para juzgar hasta que punto los estudiantes de 15 años están en capacidad de utilizar el conocimiento matemático que han acumulado para resolver problemas que encuentran en su vida diaria, uno recolectaría información sobre su capacidad para matematizar situaciones complejas. Claramente esto no es práctico. Por lo tanto, OCDE / PISA ha elegido preparar ciertos elementos para evaluar los diferentes pasos de este proceso. La siguiente sección describe la estrategia escogida para formular problemas y preguntas de examen que cubran los cinco aspectos fundamentales de la matematización. El propósito es utilizar las respuestas a estas preguntas para ubicar a los estudiantes en la escala de competencia matemática de OCDE / PISA.
ORGANIZACIÓN DEL DOMINIO
El dominio de competencia matemática de OCDE / PISA comprende tres ejes principales:
- Las situaciones o contextos en que se ubican los problemas,
- El contenido matemático que se requiere para resolver los problemas, organizado de acuerdo a ciertas nociones claves, y, sobre todo,
- Las competencias que deben ser aplicadas para conectar el mundo real, en el que se generan los problemas, con las matemáticas, para resolver así los problemas.
Estos componentes se representan gráficamente a continuación:
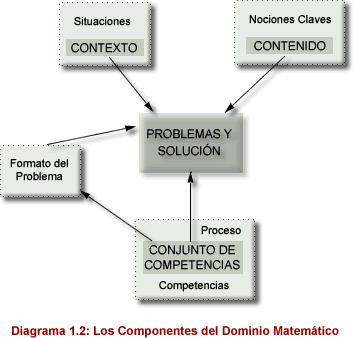
El nivel de competencia matemática de una persona se refleja en la manera en la que utiliza los conocimientos y las herramientas matemáticas para resolver problemas. Los problemas (y sus soluciones) pueden ocurrir dentro de una variedad de situaciones o contextos en la vida de cada individuo. Los problemas formulados por OCDE / PISA se refieren al mundo real en dos aspectos. Primero, los problemas se ubican dentro de situaciones relevantes a la vida del estudiante. Estas situaciones forman parte del mundo real y están representadas en el diagrama 1.2 por el cuadrado grande de la esquina superior izquierda. Asimismo, dentro de esa situación, los problemas revisten un contexto más específico. Este está representado por el cuadrado pequeño enmarcado dentro del cuadrado de situaciones.
El siguiente componente del mundo real que debe ser considerado cuando se habla de competencia matemática es el contenido matemático que la persona puede traer a colación para resolver un problema. El contenido matemático se puede dividir en cuatro categorías fundamentales que comprenden los tipos de problemas que surgen en la vida cotidiana y al mismo tiempo se refieren a la manera en que estos problemas se le presentan a la gente. Para los propósitos de la evaluación de PISA, estas nociones claves son: cantidad, espacio y forma, cambios y relaciones, e incertidumbre. Esta clasificación difiere en algo del contenido típico de los currículos escolares. Sin embargo, en su conjunto, estas nociones claves en términos generales, comprenden la totalidad de los temas matemáticos que se requiere que aprendan los estudiantes. Las nociones claves están representadas por el cuadrado grande de la esquina superior derecha del diagrama. Los contenidos que se aplican para un problema particular se extraen de estas nociones generales. Estos están representados por el cuadrado más pequeño enmarcado dentro del anterior.
Las flechas que van de “contexto” y “contenido” al problema específico demuestran como se plantea un problema tanto en el mundo real como en el campo matemático.
Los procesos matemáticos que los estudiantes aplican cuando intentan resolver un problema se denominan competencias matemáticas. Tres conjuntos de competencias sintetizan los diferentes procesos cognitivos necesarios para resolver diversos tipos de problemas. Estos conjuntos, descritos en secciones posteriores, reflejan la manera en que los procesos matemáticos se emplean normalmente para resolver problemas que surgen de la interacción de los estudiantes con el mundo que los rodea.
Así, el componente de procesos de este sistema está representado primero por el cuadrado grande de la parte baja de la gráfica que representa las competencias matemáticas generales, y el pequeño que representa los tres conjuntos específicos de competencias. Las competencias particulares que se necesitan para resolver un problema estarán relacionadas con la naturaleza de este, y se verán reflejadas en la solución planteada. Esta interrelación está representada por la flecha que conecta a los conjuntos de competencias con el problema y su solución.
La flecha restante va de los conjuntos de competencias al formato del problema. Las competencias utilizadas para resolver un problema están relacionadas a la forma del problema y sus requisitos particulares.
Es importante subrayar que los tres componentes que se acaban de precisar tienen características diferentes. Mientras que las situaciones y los contextos definen las áreas de problemas en el mundo real, y las nociones claves reflejan la manera en que miramos el mundo a través de “lentes matemáticos”, las competencias son el corazón del “alfabetismo” matemático. Solo cuando ciertas competencias estén a disposición de los estudiantes podrán estos resolver exitosamente ciertos problemas. Evaluar la competencia matemática de los estudiantes incluye evaluar hasta qué punto cuentan con habilidades cuantitativas que puedan aplicar productivamente en situaciones problemáticas.
LAS COMPETENCIAS
Para evaluar el nivel de competencia matemática de los alumnos, OCDE / PISA se basa en las ocho competencias matemáticas específicas identificadas por Niss (1999) y sus colegas daneses [2]:
- Pensar y razonar. Incluye plantear preguntas características de las matemáticas (“¿Cuántas … hay?”, “¿Cómo encontrar …?”); reconocer el tipo de respuestas que las matemáticas ofrecen para estas preguntas; distinguir entre diferentes tipos de proposiciones (definiciones, teoremas, conjeturas, hipótesis, ejemplos, condicionales); y entender y manipular el rango y los límites de ciertos conceptos matemáticos.
- Argumentar. Se refiere a saber qué es una prueba matemática y cómo se diferencia de otros tipos de razonamiento matemático; poder seguir y evaluar cadenas de argumentos matemáticos de diferentes tipos; desarrollar procedimientos intuitivos; y construir y expresar argumentos matemáticos.
- Comunicar. Involucra la capacidad de expresarse, tanto en forma oral como escrita, sobre asuntos con contenido matemático y de entender las aseveraciones, orales y escritas, de los demás sobre los mismos temas.
- Modelar. Incluye estructurar la situación que se va a moldear; traducir la “realidad” a una estructura matemática; trabajar con un modelo matemático; validar el modelo; reflexionar, analizar y plantear críticas a un modelo y sus resultados; comunicarse eficazmente sobre el modelo y sus resultados (incluyendo las limitaciones que pueden tener estos últimos); y monitorear y controlar el proceso de modelado.
- Plantear y resolver problemas. Comprende plantear, formular, y definir diferentes tipos de problemas matemáticos y resolver diversos tipos de problemas utilizando una variedad de métodos.
- Representar. Incluye codificar y decodificar, traducir, interpretar y distinguir entre diferentes tipos de representaciones de objetos y situaciones matemáticas, y las interrelaciones entre diversas representaciones; escoger entre diferentes formas de representación, de acuerdo con la situación y el propósito particulares.
- Utilizar lenguaje y operaciones simbólicas, formales y técnicas. Comprende decodificar e interpretar lenguaje formal y simbólico, y entender su relación con el lenguaje natural; traducir del lenguaje natural al lenguaje simbólico / formal, manipular proposiciones y expresiones que contengan símbolos y fórmulas; utilizar variables, resolver ecuaciones y realizar cálculos.
- Utilizar ayudas y herramientas. Esto involucra conocer, y ser capaz de utilizar diversas ayudas y herramientas (incluyendo las tecnologías de la información y las comunicaciones TICs) que facilitan la actividad matemática, y comprender las limitaciones de estas ayudas y herramientas.
NOTAS DEL EDITOR:
[1] Evaluación PISA 2003, Competencia en lectura; http://www.eduteka.org/Pisa2003.php
[2] Niss, M. (1999), Competencies and Subject Description, Uddanneise, 9, pp. 21-29.
CRÉDITOS:
Traducción realizada por EDUTEKA de algunos apartes de la sección correspondiente a “Competencias en Matemáticas” del documento “The PISA 2003 Asssessment Framework” publicado (en inglés, en formato PDF, 1.7MB) por OECD/PISA. http://www.pisa.oecd.org/
Publicación de este documento en EDUTEKA: Octubre 18 de 2003.
Última modificación de este documento: Octubre 18 de 2003.




