WebQuest Matemáticas Aritmética Solución De Ecuaciones Cuadráticas Por Su Formula General
Solución De Ecuaciones Cuadráticas Por Su Formula General
Publicado el 02 Mayo de 2021
Autor: MARIA CHICHANDE
Introducción
.
INTRODUCCIÓNEcuación cuadrática
Fórmula general
Consideremos la ecuación general de segundo grado (ecuación cuadrática) que tiene la forma: 
Cuando nos enfrentamos por primera vez en la vida a esta clase de problemas, la primera forma en la que se intenta dar una respuesta es probando con varios números hasta "atinarle" (ya sea por que nos sonría la buena fortuna, o por aproximación).
Después, conforme nos vamos enfrentando a mas problemas que involucran ecuaciones cuadráticas, descubrimos algunos métodos de solución. De los primeros que aprendemos (por simplicidad) están el "Método Gráfico" (Realizar la gráfica correspondiente a la ecuación cuadrática igualada a cero y observar en que abscisas la gráfica "toca o pasa" por el eje horizontal del plano cartesiano). Otro método que aprendemos es el "Método de Factorización" (Trabajar con la expresión cuadrática igualada a cero hasta dejarla expresada como multiplicación de otras dos expresiones algebraicas, y encontrar "por simple observación" los valores que hacen que estas últimas dos ecuaciones sean iguales a cero).
as desventajas de estos métodos es que implican trabajo excesivo, y no se garantiza que se encuentre la solución de la ecuación (al menos una solución "Real").
El último método que se estudia para resolver ecuaciones de segundo grado es la "Fórmula General".
(Puede quitar la publicidad ampliando la cuenta)
Ficha técnica
Área:Matemáticas
Asignatura:Aritmética
Edad: No hay restriccion de edad
Herramientas:
Infografías
Tarea
.
TAREAAnalizando la raíz cuadrada, se llega a las siguientes conclusiones:
Si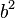 
es menor que 
los resultados de X serán dos valores con parte real y parte imaginaria. Es decir, el resultado sera un número complejo.
Si 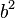es mayor que obtendremos dos valores distintos de X reales.
Y si 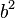es igual que obtendremos dos valores de X reales e iguales.
Al término 
se le llama discriminante.
tomando en cuenta el orden de los terminos: "a","b"y"c"=x²-6x+9
Procesos
.
PROCESOResolviendo ecuaciones cuadráticas por medio de: LA FÓRMULA GENERAL
Debes tomar en cuenta los siguientes aspectos:
Si la ecuación no está reducida entonces debemos realizar las operaciones necesarias para reducirla a la forma: ax² + bx + c = 0
Ejemplo: 4x2 - 5x + 1 = 3x2 - 7x + 4
Valores de los coeficientes:
Reduciendo: 4x2 - 5x + 1 - 3x2 + 7x - 4 = 0 x2 + 2x – 3 = 0
Valores de los coeficientes: a2 + bx + c = 0 x2 + 2x - 3 = 0 a = 1 b = 2 c = - 3
Aplicando la Fórmula General Para resolver cualquier ecuación cuadrática puede utilizarse La siguiente fórmula, conocida como: Fórmula General
Con la ecuación x2 + 2x - 3 = 0
Sustituimos los valores en la fórmula general :
a = 1
b = 2
c= - 3
Realizando la operación:
1. Resolvemos las operaciones de la raíz
1.-
2.-
3.-
Significado del signo ±
En las ecuaciones de segundo grado se obtienen dos Soluciones:
- una la obtendremos usando el signo +
- y otra usando el signo –
Las cuales se obtienen por separado. Signo + 
Signo – 
Recursos
.
RECURSOSTUTORIAL 1
VIDEO
https://www.youtube.com/watch?v=gYNvguREGsQ&feature=youtu.be
fuentes:
http://eca-algebra-3-medio.blogspot.mx/2010/08/ejercicios-aplicando-la-formula-general.html
https://www.youtube.com/watch?v=jsT6Oy5CooQ
http://es.slideshare.net/matematicasec29/ecuacion-de-formula-general?related=1
https://es.wikibooks.org/wiki/Ecuaci%C3%B3n_cuadr%C3%A1tica/F%C3%B3rmula_general
http://www.profesorenlinea.com.mx/matematica/Ecuaciones_Seg_grado.html
Evaluación
.
EVALUACIÓNEJERCIO 1
x² - 3x + 2 = 0;
X² - 3x + 2 = 0 En este caso:
a = 1, b= - 3, c = 2. Luego
EJERCICIO 2
4x² + 12x + 9 = 0;
4x² + 12x + 9 = 0.
En este caso:
a = 4, b= 12, c = 9. Luego
EJERCICO 3
9x² + 18x + 17 = 0;
9x² + 18x + 17 = 0.
En este caso:
a = 9, b = 18, c = 17. Luego
EJERCICO4
6u (2 – u ) = 7;
6u (2 – u) = 7.
12u–6u²=7=> 6u²-12u–7 =0
En este caso:
a = 6, b =- 12, c = - 7. Luego
Notas
Cada ejercicio de la evaluación debe ser presentado con su respectivo proceso y repuesta.
*Nota: toda la información que aparece en los Proyectos de Clase y WebQuest del portal educativo Eduteka es creada por los usuarios del portal.