Requisitos

1. Tener nociones de geogebra para gráficar funciones cuadráticas.

2. Tener conocimientos previos de factorizacion algebraica. (Completacion de cuadrados).

Proceso

El proposito de esta actividad recae netamente en que el alumno sepa graficar una funcion cuadratica en el eje cartesiano y use recursos que ayuden a hacer el trabajo mas facil.

Esta actividad esta enfocada a sacar el vertice y los puntos de interseccion con el eje x.

Actividades Docente

Una función cuadrática es un polinomio de grado 2, es decir, el exponente más alto en la variable es 2. Los siguientes son ejemplos de funciones cuadráticas:

La función cuadrática más básica y simple tiene la ecuación . Si hacemos una tabla con los valores de esta función, vemos que el rango (los valores de y, o salida) no se comportan como una función lineal. En una función lineal, el valor de y cambia por la misma cantidad cada vez que el valor de x aumenta por 1. Eso no sucede con una función cuadrática:

Los valores de y no cambian por una cantidad constante. Grafiquemos algunos puntos para ver cómo se vería la función:

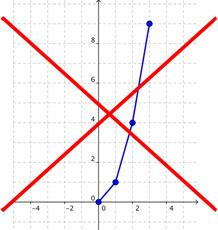
Después de graficar algunos puntos, podría ser tentador conectar los puntos con segmentos de línea, que son rectos. Pero esto estaría mal, y produciría un patrón que no representa la función.

Borremos esas líneas rectas y grafiquemos el resto de los puntos:

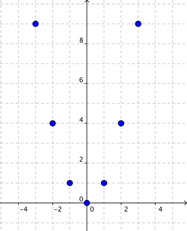
Ahora dibujamos una curva suave conectando los puntos.

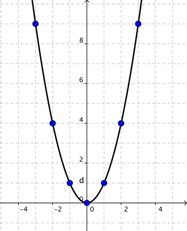
¡Mejor! Una función cuadrática resulta en una gráfica con forma de U, llamada parábola. Los valores de la función cambian suavemente, por lo que la curva debe ser suave también. Ahora que podemos ver la naturaleza de la parábola (forma de U), veamos su forma en detalle.

La forma estándar de una ecuación cuadrática es . Por ejemplo , el valor del coeficiente a es 1, y b y c son 0. Si bien muchas ecuaciones cuadráticas presentan valores de b y c diferentes de cero, la gráfica resultante siempre será una parábola.

Las parábolas tienen muchas propiedades que pueden ayudarnos a graficar ecuaciones cuadráticas. Una parábola tiene un punto especial llamado vértice; este es el punto donde la U "da la vuelta". Nota que en el vértice, la parábola cambia de dirección:

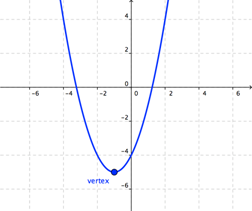
El vértice es el punto más alto o más bajo de la curva, dependiendo si la U se abre hacia arriba o hacia abajo. En el caso de que la parábola abra hacia arriba, el vértice será su punto más bajo; y una parábola que abre hacia abajo, tendrá un vértice en su punto más alto.

Todas las funciones parabólicas tienen un eje de simetría vertical, una línea imaginaria que pasa a través de la mitad de la forma de U y la divide en dos mitades que son imágenes de espejo una de la otra. El eje de simetría siempre pasa por el vértice. Cualquier par de puntos con el mismo valor de y estarán a la misma distancia del eje. En la gráfica interactiva siguiente, haz clic y arrastra el punto A y ve cómo se mueve el punto A'. Nota que el eje de simetría actúa como un espejo entre A y A’.

egefdsfsdfeeegegEjD=b2−4acD=b2−4acD=b2−4acD=b2−4acdfdf

Actividades Estudiante

Graficar la siguiente función cuadrática:

y = x² – 4x + 3.

y = x² –2x + 3.

y = x² -4x + 4

Evaluación

Las evaluaciones para el tema de funciones cuadráticas se realizara en cuanto a una pauta de evaluación de este proyecto en el cual estan explicitos cada uno de los pasos que el estudiante debe completar para una óptima resolución del ejercicio.

A Continuación se presentara un ejercicio propuesto en el cual se abordara toda la materia de las clases anteriores.

Analice la concavidad de la siguiente función , encuentre su vértice , para analizar la naturaleza de sus raíces utilice el discriminante. Grafique la funcion con todos los componentes anteriormente pedidos. Al finalizar el ejercicio grafique la misma funcion en geogebra y compare sus resultados.

Ejercicio :

f(x) = −x² + 4x − 3

Notas

Se añaden videos de youtube en los cuales se estimula la motivacion del estudiante , en base a clases expositivas las cuales consideran ejercicios de menor y mayor complejidad. La informacion fue extraida de internet en gran mayoria para lo cual se analizo el nivel en que se profundizaría en el proyecto teniendo en cuenta los programas de estudio.

El programa geogebra en el trascurso de curso se hace enfasis en usarlo para graficar y de hecho se incluye un video de como graficar una funcion en geogebra de modo que el alumno pueda corroborar resultados y asimilar de manera significativa el aprendizaje 

Los ejercicios propuestos en sesiones se han desarrollado con antelacion en las mismas sesiones solo que con numeros distintos.

El sistema de redes a facilitado la ejecucion de tareas a distancia , por la cual se a creado este curso que abarca desde conceptos basicos en adelante.