Proyecto Tecnología e Informática Informática Herramientas Ludicas En La Comprensión Y Aplicacion De Las Matemáticas
Herramientas Ludicas En La Comprensión Y Aplicacion De Las Matemáticas
Publicado el - - -
Autor: GRACIELA MONSALVE MONSALVE
Descripción
JUSTIFICACION
Hoy día, la sociedad Colombiana está demandando que lo resultados de aprendizaje de los niños mejoren en Lenguaje, Matemáticas y Ciencias. Hay una gran preocupación por la calidad académica en cuanto a competencias y saberes básicos de los que están egresando, en particular por su formación en el ramo de matemáticas.
El desarrollo de la educación de nuestro país está en uno de los momentos importantes de la presente década, es por esto que el ministerio de Educación Nacional ha venido buscando respuesta a tantas inquietudes de carácter educativo que surgen en el contexto con respecto a lo pedagógico, metodológico y el saber específico de cada una de las área que comprende el sistema escolar de nuestro país; en la misma tarea se encuentran la mayoría de instituciones educativas buscando la manera de dar respuesta a tantos cambios que se producen en el campo de lo educativo en el mundo de hoy.
Todo este trabajo se realiza con el único propósito de mejorar el quehacer diario del maestro, a partir de entender que como docentes debemos generar diferentes estrategias de orden didáctico y pedagógico que motiven el aprendizaje tanto del mismo docente como de nuestros estudiantes; para poder dar respuesta a las necesidades y competencias matemáticas que el mundo hoy por hoy está exigiendo en el campo laboral.
Creemos que uno de los elementos importantes para dar respuesta a todo lo anterior es el trabajo en equipo, entendiendo al equipo como un grupo de seres humanos que están creciendo juntos cada día y están buscando las mejores estrategias investigativas, didácticas, y pedagógicas para llevar al aula de clase compartir con sus estudiantes y lograr los mejores aprendizajes. Un equipo de trabajo no escatima esfuerzos en dar lo mejor de sí para que cada tarea que se emprenda arroje los mejores resultados, para que el compartir conocimiento, construir nuevas ideas pedagógicas, investigar nuevos hechos en el mudo de la educación se convierta en el norte del compromiso como docentes, destacando ante todo esa capacidad de desprendimiento de cualquier tipo de Tabú, temor, egoísmo en el momento de ejecutar nuestro trabajo de aula y abrirnos la puerta unos a otros para que el colega que desee ingrese allí y nos ayude a mejorar cada día nuestro que hacer educativo desde su Experiencia, su saber específico, saber pedagógico y ante todo desde su capacidad humana de entender que tenemos la responsabilidad de entregar todo nuestro esfuerzo, sacrificio y experiencia por el bien de los Jóvenes de hoy que tanto lo necesitan.
La matemática ha sido rodeada de un sinnúmero de paradigmas y hasta cierto punto de un manto de misterio e incomprensión.
Numerosos son los intentos por incluir la lúdica a la enseñanza de las matemáticas como un factor integrado en la construcción de conocimiento matemático, aprovechando de paso, la importancia que la Ley General de la educación otorga a la actividad lúdica en el proceso de cambio que vive el país en materia de educación.
Los conceptos para describir los usos y aplicaciones de la lúdica son diversos, sin embargo, estos no se limitan únicamente a la física de los cuerpos y a las cosas, sino sobre todo estudian la relación de estos lenguajes lúdicos con los mecanismos de producción.
La apertura de espacios, de establecimientos de nuevos nexos entre los individuos y las cosas, constituye un movimiento de fuga en cuanto accedemos a nuevas actividades antes consideradas ajenas al juego.
Los discursos, los contextos semánticos que provee la cultura, la combinación de actividades produce nuevos juegos y nuevas actitudes. La energía acumulada y liberada en el juego opera como una máquina de significación y re codificación del mundo.
Para los maestros en general, es importante, apoyar en la práctica, la importancia que la nueva norma otorga a la lúdica en la educación.
Los niños, a medida que va creciendo, según Rafael Porlan, construyen nuevos significados a partir de los anteriormente preexistentes y en interacción con su experiencia física, social y cultural (1995- 63).
Los niños en este sentido poseen preconceptos, pretorías, saberes idiosincráticos que les permiten organizar y actuar sobre el mundo.
De los tres años en adelante el juego implica para el niño alto grado de significación social: los niños a través del juego cotidiano, empiezan a interiorizar y a construir sus valores sociales, éticos y morales como también a construir los conocimientos que guaran su futuro.
Como maestros no podemos dejar de lado estos conceptos sino que debemos incorporarlos a nuestras estrategias para la construcción de saberes.
La matemática ofrece un conjunto amplio de procedimientos de análisis, modelación, cálculo, medición y estimación del mundo natural y social, que permite establecer relaciones entre los más diversos aspectos de la realidad, no sólo cuantitativas y espaciales, sino también cualitativas y predictivas.
El juego en el aprendizaje
Introducir el juego de las palabras a la escuela como una actividad cultural que logre un proceso de mediación entre la fantasía y la realidad, entre el pensamiento y el lenguaje, entre la libertad y sueño, entre goce y placer, más que necesario es urgente.
El niño comienza jugando con sus fantasías y con su propio cuerpo, manos y dedos; juega con el espacio, con el tiempo, con los objetos, con el contexto, con el lenguaje y con los elementos tecnológicos que están hoy a su alcance.
En este último espacio es donde el docente debe sacar el máximo provecho a las apreciaciones anteriores.
Si en juego se utiliza el concepto de cantidad, inconscientemente se apropia del sentido de cálculo y al organizar el balance definitivo de sus juegos, estará poniendo en práctica conocimientos matemáticos que posteriormente el docente afianzara con el manejo de algoritmos.
Existe un sin número de juegos donde se requiere que el estudiante necesariamente calcule. Al principio lo hará muy lentamente, pero a medida que el juego avanza, el estudiante le dará más importancia a los resultados por lo que se concentrara en las cuentas que en ultimas determinara quien es el ganador y a ellos más que a nadie les interesa tener claro cuales ganaron y porque.
Pero en este aspecto el docente debe cuidarse de no caer en la rutina. Un juego puede desarrollarse de muchas formas y en el transcurso del mismo se pueden aplicar variables concertadas con los estudiantes cuando estén perdiendo motivación.
Ficha técnica
Área:Tecnología e Informática
Asignatura:Informática
Edad: - No hay restriccion de edad
Duración:
Herramientas:
Diagramas de flujo - proceso
Objetivos
OBJETIVOS
Objetivo general:
· Vincular, en lo posible, los contenidos matemáticos a propósitos e intenciones humanas y situaciones significativas.
Objetivos específicos:
· Contextualizar los esquemas matemáticos hacia niveles de abstracción con cierta complejidad a partir del ritmo exigido por el alumno.
· Asegurar la asimilación de preconceptos antes de pasar un aprendizaje significativo, afianzando la generalización de los procedimientos y contenidos.
· Asegurar el dominio y enriquecimiento de los códigos de representación asegurando que la traducción entre el lenguaje verbal y los códigos matemáticos, puedan realizarse con destreza
· Servirse de la atención exploratoria del sujeto y asegurar su atención selectiva sólo en periodos en que ésta puede ser mantenida.
· Ejercitar de manera sistemática el uso y selección de los recursos cognitivos.
· Recordar los aspectos relevantes de una tarea o problema y procurar comprobar que no se exige más de lo que permite la competencia lógica del alumno.
· Ejercitar de manera sistemática las estrategias y algoritmos específicos que exigen las tareas.
· Procurar al niño tareas de orientación adecuada, procedimientos de análisis profundo y ocasiones frecuentes de aprendizaje incidental.
· Valorar y motivar a los niños que no parezcan interesados o competentes.
Recursos
RECURSOS.
RECURSOS HUMANOS
- ESTUDIANTES
- DOCENTES
- DIRECTIVOS
- PADRES DE FAMILIA
RECURSOS FISICOS
- SALA DE INFORMATICA
- MATERIAL DIDACTICO
- HARDWARE
- SOFTWARE EDUCATIVO
- TEXTOS
- CARTELERAS
- IMPRESORAS
- SCANNER
- PROYECTOR DE VIDEO
- DVD
- TELEVISOR
RECURSOS FINANCIEROS
- APORTES DE LOS ESTUDIANTES
- APORTES DE LA INSTITUCION
RECURSOS TECNICOS
- CONOCIMIENTOS SOBRE TECNOLOGIA E INFORMATICA
- INTERNET
Requisitos
.Contenidos
Recursos
Geometría-Transformaciones: Uso de regla y compás; de escuadra y transportador; manejo de un programa computacional que permita dibujar y transformar figuras geométricas.
Números y proporcionalidad: Resolución de desafíos y problemas numéricos, tales como cuadrados mágicos o cálculos orientados a la identificación de regularidades numéricas.
Algebra y funciones: Análisis de fórmulas de perímetros, áreas y volúmenes en relación con la incidencia de la variación de los elementos lineales y viceversa.
Geometría: Análisis de la posibilidad de embaldosar el plano con polígonos. Aplicación de las transformaciones geométricas en las artes por ejemplo MC Escher
P r o c e s a d o r Geométrico (Cabri Geométrico) Esta herramienta permite dibujar y trabajar con figuras geométricas, rotarlas, etc.
Software «El cumpleaños» del CD Recursos Educativos Procesador de texto Este software contiene en su sección entretenciones, juegos matemáticos, cubos mágicos, construcciones, etc. Estas actividades las puede trabajar directamente o extraerlas para confeccionar una guía en el procesador de texto.
Diseñador de presentaciones
El procesador de texto y el diseñador de presentaciones, son valiosas herramientas para diseñar material didáctico que contenga figuras, dónde se pueda representar áreas o mostrar en simulaciones con diversas figuras.
Internet para obtener software educativo «Tesselmania» Existe un software de teselación llamado «Tessemania» de la empresa MECC, disponible en Internet y que puede ser utilizado como herramienta de apoyo en este sector. En Internet se encuentran ejemplos de este concepto en las artes.
Proceso
JUSTIFICACION
Hoy día, la sociedad Colombiana está demandando que lo resultados de aprendizaje de los niños mejoren en Lenguaje, Matemáticas y Ciencias. Hay una gran preocupación por la calidad académica en cuanto a competencias y saberes básicos de los que están egresando, en particular por su formación en el ramo de matemáticas.
El desarrollo de la educación de nuestro país está en uno de los momentos importantes de la presente década, es por esto que el ministerio de Educación Nacional ha venido buscando respuesta a tantas inquietudes de carácter educativo que surgen en el contexto con respecto a lo pedagógico, metodológico y el saber específico de cada una de las área que comprende el sistema escolar de nuestro país; en la misma tarea se encuentran la mayoría de instituciones educativas buscando la manera de dar respuesta a tantos cambios que se producen en el campo de lo educativo en el mundo de hoy.
Todo este trabajo se realiza con el único propósito de mejorar el quehacer diario del maestro, a partir de entender que como docentes debemos generar diferentes estrategias de orden didáctico y pedagógico que motiven el aprendizaje tanto del mismo docente como de nuestros estudiantes; para poder dar respuesta a las necesidades y competencias matemáticas que el mundo hoy por hoy está exigiendo en el campo laboral.
Creemos que uno de los elementos importantes para dar respuesta a todo lo anterior es el trabajo en equipo, entendiendo al equipo como un grupo de seres humanos que están creciendo juntos cada día y están buscando las mejores estrategias investigativas, didácticas, y pedagógicas para llevar al aula de clase compartir con sus estudiantes y lograr los mejores aprendizajes. Un equipo de trabajo no escatima esfuerzos en dar lo mejor de sí para que cada tarea que se emprenda arroje los mejores resultados, para que el compartir conocimiento, construir nuevas ideas pedagógicas, investigar nuevos hechos en el mudo de la educación se convierta en el norte del compromiso como docentes, destacando ante todo esa capacidad de desprendimiento de cualquier tipo de Tabú, temor, egoísmo en el momento de ejecutar nuestro trabajo de aula y abrirnos la puerta unos a otros para que el colega que desee ingrese allí y nos ayude a mejorar cada día nuestro que hacer educativo desde su Experiencia, su saber específico, saber pedagógico y ante todo desde su capacidad humana de entender que tenemos la responsabilidad de entregar todo nuestro esfuerzo, sacrificio y experiencia por el bien de los Jóvenes de hoy que tanto lo necesitan.
La matemática ha sido rodeada de un sinnúmero de paradigmas y hasta cierto punto de un manto de misterio e incomprensión.
Numerosos son los intentos por incluir la lúdica a la enseñanza de las matemáticas como un factor integrado en la construcción de conocimiento matemático, aprovechando de paso, la importancia que la Ley General de la educación otorga a la actividad lúdica en el proceso de cambio que vive el país en materia de educación.
Los conceptos para describir los usos y aplicaciones de la lúdica son diversos, sin embargo, estos no se limitan únicamente a la física de los cuerpos y a las cosas, sino sobre todo estudian la relación de estos lenguajes lúdicos con los mecanismos de producción.
La apertura de espacios, de establecimientos de nuevos nexos entre los individuos y las cosas, constituye un movimiento de fuga en cuanto accedemos a nuevas actividades antes consideradas ajenas al juego.
Los discursos, los contextos semánticos que provee la cultura, la combinación de actividades produce nuevos juegos y nuevas actitudes. La energía acumulada y liberada en el juego opera como una máquina de significación y re codificación del mundo.
Para los maestros en general, es importante, apoyar en la práctica, la importancia que la nueva norma otorga a la lúdica en la educación.
Los niños, a medida que va creciendo, según Rafael Porlan, construyen nuevos significados a partir de los anteriormente preexistentes y en interacción con su experiencia física, social y cultural (1995- 63).
Los niños en este sentido poseen preconceptos, pretorías, saberes idiosincráticos que les permiten organizar y actuar sobre el mundo.
De los tres años en adelante el juego implica para el niño alto grado de significación social: los niños a través del juego cotidiano, empiezan a interiorizar y a construir sus valores sociales, éticos y morales como también a construir los conocimientos que guaran su futuro.
Como maestros no podemos dejar de lado estos conceptos sino que debemos incorporarlos a nuestras estrategias para la construcción de saberes.
La matemática ofrece un conjunto amplio de procedimientos de análisis, modelación, cálculo, medición y estimación del mundo natural y social, que permite establecer relaciones entre los más diversos aspectos de la realidad, no sólo cuantitativas y espaciales, sino también cualitativas y predictivas.
El juego en el aprendizaje
Introducir el juego de las palabras a la escuela como una actividad cultural que logre un proceso de mediación entre la fantasía y la realidad, entre el pensamiento y el lenguaje, entre la libertad y sueño, entre goce y placer, más que necesario es urgente.
El niño comienza jugando con sus fantasías y con su propio cuerpo, manos y dedos; juega con el espacio, con el tiempo, con los objetos, con el contexto, con el lenguaje y con los elementos tecnológicos que están hoy a su alcance.
En este último espacio es donde el docente debe sacar el máximo provecho a las apreciaciones anteriores.
Si en juego se utiliza el concepto de cantidad, inconscientemente se apropia del sentido de cálculo y al organizar el balance definitivo de sus juegos, estará poniendo en práctica conocimientos matemáticos que posteriormente el docente afianzara con el manejo de algoritmos.
Existe un sin número de juegos donde se requiere que el estudiante necesariamente calcule. Al principio lo hará muy lentamente, pero a medida que el juego avanza, el estudiante le dará más importancia a los resultados por lo que se concentrara en las cuentas que en ultimas determinara quien es el ganador y a ellos más que a nadie les interesa tener claro cuales ganaron y porque.
Pero en este aspecto el docente debe cuidarse de no caer en la rutina. Un juego puede desarrollarse de muchas formas y en el transcurso del mismo se pueden aplicar variables concertadas con los estudiantes cuando estén perdiendo motivación.
Actividades Docente
.Acciones:
El docente explica algunos terminos que son necesarios para el proyecto.
Teselaciones
Una teselación es cuando cubres una superficie con un patrón de formas planas de manera que no se superponen ni hay huecos.
Ejemplos:
 |
 |
 |
||
|
Rectángulos
|
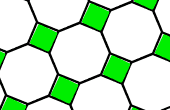
Octágonos y cuadrados
|
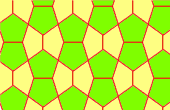
Pentágonos
|
Teselaciones regulares
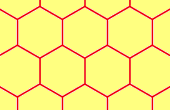
Una teselación regular es un patrón que se consigue repitiendo un polígono regular. Sólo existen 3 teselaciones regulares:
 |
 |
 |
||
|
Triángulos
|
Cuadrados
|
Hexágonos
|
||
|
3.3.3.3.3.3
|
4.4.4.4
|
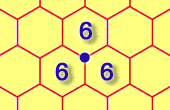
6.6.6
|
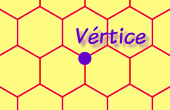
Fíjate en un vértice...
|
||
|
||
|
En una teselación regular, ¡el patrón es el mismo en todos los vértices! |
Teselaciones semi-regulares
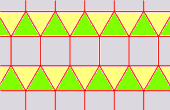
Una teselación semi-regular está hecha con dos o más polígonos regulares. ¡El patrón debe ser el mismo en todos los vértices! Sólo existen 8 teselaciones semi-regulares:
 |
 |
 |
||
| 3.3.3.3.6 | 3.3.3.4.4 | 3.3.4.3.4 | ||
 |
 |
 |
||
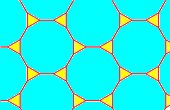
| 3.4.6.4 | 3.6.3.6 | 3.12.12 | ||
 |
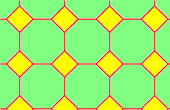 |
|||
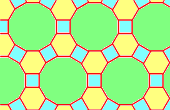
| 4.6.12 | 4.8.8 | |||
|
Para darle un nombre a una teselación, da la vuelta a un vértice y escribe cuántos lados tiene cada polígono en orden... por ejemplo "3.12.12". |
|
| Y siempre se empieza por un polígono que tenga el mínimo número de lados, así que es "3.12.12", no "12.3.12" | |
| Pregunta: En las teselaciones de arriba, ¿el patrón es el mismo en todos los vértices? |
Otras teselaciones
También existen otros tipos de teselaciones, como las "demiregulares", ¡pero los matemáticos todavía no se han puesto de acuerdo en cuáles son esas exactamente!
Y también se pueden permitir formas curvas (no sólo polígonos) con lo que tienes teselaciones como estas:
 |
 |
 |
||
|
Formas curvas
|
Círculos
|
¿Águilas?
|
Se inicia la sesión formando grupos de dos o tres alumnos por computador.
El profesor comienza con una introducción sobre el tema que muestra algunos dibujos de M. C. Escher, representativos de teselaciones. Para ésto, puede llevar a los estudiantes a navegar online por la galería de Escher en Internet donde están publicados sus dibujos http://www.worldofescher.com/gallery/)
o tener previamente bajadas las imágenes en el disco local. Son buenos ejemplos de teselaciones: «Symmetry E70. Butterflies», una teselación hecha con mariposas y «Metamorphose II» un lienzo de mutaciones contínuas.
Actividades Estudiante
.Se solicita a los grupos construir sus propias teselaciones en el computador, usando un programa llamado «Applets Pattern Blocks», escrito en lenguaje java y disponible para ejecutarse desde Internet en la dirección http://www.best.com/~ejad/java/patterns/patterns_j.shtml.
Las funciones de este programa son muy simples y se explican en Anexos. Específicamente, se les pide que manipulen triángulos, cuadrados, hexágonos, trapecios y rombos, para ver como pueden combinarse formando patrones que cubran todo el plano. Se sugiere a los grupos que comiencen haciendo patrones con una sola figura (triángulo, o cuadrado, o rombo, etc.) y que impriman una copia de su trabajo.
Luego, que continúen haciendo patrones pero ahora con dos figuras distintas (triángulo y rombo, trapecio y hexágono, etc.) y también las impriman.
Finalmente, se pide realicen la misma actividad con tres figuras distintas. Es deseable que cada grupo llegue al menos a realizar dos patrones con 1, 2 ó 3 figuras distintas. Después de construidas las teselaciones, cada grupo de alumnos con las hojas impresas de sus trabajos, deberá determinar: cuáles de los patrones son teselaciones y cuáles no lo son, usando la definición de teselación, cuáles de los patrones son teselaciones regulares y cuáles son semiregulares, y cuál es el patrón base que determina una teselación regular y una irregular, de acuerdo a sus trabajos realizados. El profesor deberá verificar que todos los grupos realicen teselaciones de distinto tipo en sus trabajos. Más tarde, se rotan los trabajos de los grupos para que aprecien más ejemplos de teselaciones. Además, se aprovecha la oportunidad para discutir brevemente sobre las clasificaciones hechas por los compañeros: teselación o no, regular o no y el patrón que se considera base. La idea es, que los estudiantes hagan algunas conjeturas de cómo se pueden construir teselaciones. Por ejemplo, en el caso de las teselaciones regulares, es posible llegar a la conclusión que no sirven cuadrilateros cóncavos para su construcción, o que los polígonos regulares que sirven para teselar son aquellos cuyo ángulo interior es un múltiplo de 360º, etc.
Evaluación
Construyan una teselación regular con el programa de Applets e imprima una copia.
Construyan una teselación semi-regular con el programa de Applets e imprima una copia.
Determinen si los siguientes patrones son teselaciones.
Justifique su respuesta.
Notas
.CARACTERIZACIÓN DE LA INSTITUCIÓN
El colegio Ofelia Uribe de Acosta se encuentra ubicado en la calle 81 A Sur # 6-40 Este, localidad quinta de usme en el barrio Alfonso López, atiende a 2600 alumnos vecinos de la localidad en un 90% corresponden a estratos socioeconómicos 1 y 2. El colegio cuenta con dos sedes, la sede A es una edificación inaugurada en el 2007 con 20 salones con inmobiliario distribuidos en cuatro niveles diferentes de dos pisos cada uno, salas especializadas para tecnología y sistemas, laboratorios de biología Química y Física, dos canchas polideportivas y servicio de comedor escolar.
Agradecimientos a los Docentes : Fredy Saúl Clavijo Rojas, Lino Alberto Nieto.

*Nota: toda la información que aparece en los Proyectos de Clase y WebQuest del portal educativo Eduteka es creada por los usuarios del portal.