Inicio Actividades Otra Folleto de secciones transversales
Folleto de secciones transversales
Folleto de secciones transversales
¿En qué consiste la actividad Folleto de secciones transversales ?
Las secciones transversales son las representaciones bidimensionales formadas en la intersección de un objeto tridimensional y un plano que lo corta.La sección transversal es la porción del objeto que se muestra en el corte. Estas secciones tienen propiedades interesantes y ayudan a comprender mejor los conos, cilindros y poliedros. En particular, las secciones cónicas son secciones transversales de un cono o un doble cono. Pueden explorarse en profundidad con la aplicación Folleto de cónicas.
En esta aplicación usted podrá explorar secciones cónicas de varios conos, cilindros, prismas y pirámides. Al cambiar las propiedades del objeto tridimensional y observar las diferentes secciones transversales, descubrirá nuevas maneras de crear una variedad de objetos familiares. Las secciones transversales se muestran en una gráfica bidimensional a la derecha del objeto tridimensional, para ayudarle a visualizarlas.
La transición entre los espacios bi- y tri- dimensional es una habilidad importante. Mientras practica con esta aplicación, asegúrese de entender cómo cada representación gráfica se deriva del objeto tridimensional.
Recursos para la clase
- Actividad Trabajando con cónicas
- Discusión sobre Secciones transversales
- Discusión sobre Introducción al plano de coordenadas y a las coordenadas
- Taller Folleto de secciones transversales Preguntas de exploración
- Taller Folleto de secciones transversales Preguntas de exploración (doc).
Actividad
¿Cómo puedo utilizar esta actividad?
Descripción
Esta aplicación le permite al usuario explorar el mundo de las transformaciones, reflexiones y rotaciones. Le permite transformar polígonos con hasta 12 vértices, de coordenadas definidas por el usuario.
Controles y Resultados
Esta actividad permite que el usuario genere secciones transversales de variados sólidos usando botones y barras deslizantes para seleccionar el tipo de sólido, su tamaño y la posición del corte. El contorno de cada sección transversal se dibuja en el gráfico a medida que se forma.
A la izquierda de la página está el sólido predeterminado, que es el doble cono. Al lado derecho hay una gráfica que muestra la sección transversal predeterminada de una elipse
Botones Zoom/Desplazamiento. En la esquina superior derecha del gráfico hay tres botones con imágenes de lupas. De arriba a abajo, representan acercamiento, alejamiento y desplazamiento, respectivamente.
- Para un zoom de acercamiento haga click en el botón superior para activarlo y después haga click y arrastre sobre el área de la gráfica que se quiere magnificar. Las imágenes siguientes muestran primero el proceso de arrastrar con el ratón una caja alrededor de un área (izquierda) y después la imagen ampliada cuando se libera el botón del ratón (derecha). Observe que despues de que se ha ejecutado el acercamiento, el botón de la parte superior derecha ya no se ve seleccionado.
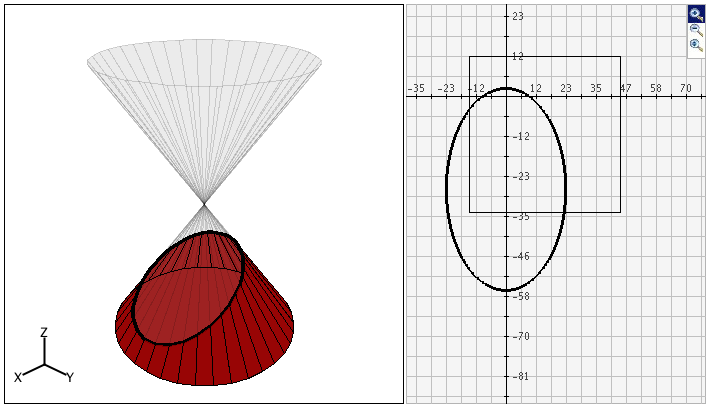
- Para disminuir el zoom, simplemente active el segundo de los tres botones. La gráfica se disminuirá automáticamente al duplicarse los valores máximo y mínimo de los ejes.
- Para usar la funcion de desplazamiento, haga click en el tercer boton para activarlo. Haga click y arrastre sobre la gráfica y se obtendrá el desplazamiento conforme al movimiento del ratón. Al aflojar la presión sobre el ratón se libera también el botón de desplazamiento.
Para cambiar el ángulo de vista del sólido puede hacerse click y arrastrar sobre él.
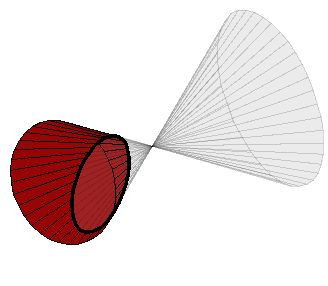
Usted puede o restablecer la vista o restablecer el gráfico, haciendo click en los botones correspondientes, que están debajo del área de visualización. Estos botones hacen que la vista o el gráfico se restablezcan a su estado original según el caso. Pero no restablecen la sección transversal.
La caja de verificación que hay abajo del sólido permite identificar la clase de sección transversal generada por el corte. Si la caja no se ha chequeado, no aparece la identificacion; cuando se chequea, aparecerá el nombre de la sección transversal: círculo, elipse, hipérbola, parábola, pentágono, etc.

El usuario puede seleccionar el tipo de sólido deseado utilizando los botones de radio situados en la parte inferior izquierda de esta página.
- El doble cono es un objeto tridimensional formado por dos conos conectados por sus vértices.
- El cono es un objeto tridimensional cuya base es un círculo y cuya superficie lateral se forma al rotar un triángulo rectángulo sobre uno de sus catetos situado en el centro del círculo y perpendicular a este. El punto extremo del cono se llama vértice.
- El cilindro es un objeto tridimensional que tiene dos bases circulares paralelas y congruentes.
- La pirámide es un objeto tridimensional que tiene como base un polígono regular y como superficies laterales triángulos con un vértice común. En un polígono regular todos los lados tienen igual longitud. El número de lados de la base puede variar de 3 a 12.
- El prisma es un objeto tridimensional que tiene dos bases paralelas y congruentes que son polígonos regulares y cuyas caras laterales son rectángulos. El número de lados de la base puede variar de 3 a 12 .
Se pueden usar las barras deslizantes para rotar el corte (alrededor del eje y o del eje z), moverlo hacia arriba o hacia abajo, o cambiar las dimensiones del sólido. Si se trata de un doble cono, un cono o un cilindro, la barra deslizante para el radio cambiará el radio del círculo de la base.
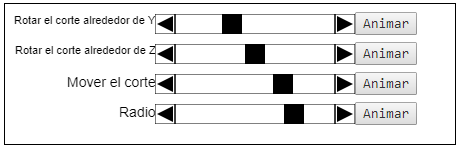
Si el sólido es una pirámide o un prisma, la barra deslizante de las caras laterales permite aumentar o disminuir el número de lados de la base del sólido. Esto cambia también el número de caras laterales.
El botón de animación en el extremo de cada barra deslizante se puede usar para mover la barra automáticamente entre sus extremos.
El usuario puede elegir cómo se muestra gráficamente la sección transversal, escogiendo cómo están determinados los ejes del gráfico. Haciendo click en los botones de radio que aparecen en la base de la aplicación puede elegir centrar los ejes en el punto más cercano al origen, en el foco de la sección cónica (sólo cuando esté trabajando con el cono, el doble cono o el cilindro) o en el centroide de la sección transversal. También puede elegir entre no tener cuadrícula o tenerla de líneas claras u oscuras.

Recursos y contexto curricular
Esta actividad le permite al usuario explorar con diferentes secciones transversales de conos, cilindros, prismas y pirámides. Las secciones transversales pueden ser difíciles de entender por el estudiante, dado que el concepto exige alternar entre figuras tri-dimensionales y su representación bidimensional .
En tanto que esta actividad fue diseñada para ayudar a los estudiantes a crear y visualizar secciones transversales de diferentes sólidos, algunos estudiantes se pueden beneficiar desarrollando actividades prácticas en las que físicamente rebanen varios sólidos antes de que intenten exploraciones de carácter más abstracto, como esta aplicación, por ejemplo.
Esta actividad debe funcionar adecuadamente con grupos de dos a cuatro estudiantes por un tiempo de 25 a 30 minutos si se utilizan las preguntas de exploración y de cinco minutos por tipo de función, en otro caso.
Ubicación en el currículo de matemáticas
- Mostrar la relación entre objetos tridimensionales y representaciones bidimensionales.
- desarrollar la habilidad para visualizar movimientos en objetos de dos y de tres dimensiones.
- Apoyar a los estudiantes en la transición del pensamiento concreto al pensamiento abstracto.
Estándares alcanzados
Grados 9-12
- Geometría
- Analizar las características y propiedades de objetos geométricos bi- y tri- dimensionales y desarrollar argumentos sobre relaciones geométricas.
- Usar visualización, razonamiento espacial y modelamiento geométrico para resolver problemas.
Esté preparado para:
- explicar cómo se conectan las dos representaciones
- explicar cómo predecir la forma que tendrá la sección transversal en una gráfica.
- Experimentar con el corte de sólidos para formar secciones transversales.
Recursos para clases
- Actividad Trabajando con cónicas
- Discusión sobre Secciones transversales
- Discusión sobre Introducción al plano de coordenadas y a las coordenadas
- Lección sobre Secciones transversales
- Taller Folleto de secciones transversales Preguntas de exploración
- Taller Folleto de secciones transversales Preguntas de exploración (doc).
