Inicio Actividades Otra Recursión
Recursión
Recursión
¿En qué consiste la actividad Recursión ?
Esta actividad le permite al usuario graficar hasta tres funciones recursivas a la vez.
En una ecuación recursiva, cada valor un depende del valor inmediatamente anterior un-1. El n es un contador para saber cuál valor sigue después de cuál. Entonces, se dice que el valor inicial es u0, donde n=0. El valor siguiente es u1, el siguiente es u2 y así sucesivamente. Una vez establecido el valor inicial, u0, se hace un determinado cálculo con él para obtener u1. El mismo cálculo se hace con u1 para obtener u2, con este para obtener u3 y así sucesivamente.
Por ejemplo, consideremos la ecuación recursiva un = un-1 + 2 con valor inicial u0 =0. Para encontrar u1 utilizamos la ecuación y hacemos n=1. Entonces u1 = u1-1 + 2 = u0 + 2 = 0 + 2 = 2. Por lo tanto u1 = 2. Para encontrar u2 utilizamos el valor de u1 y encontramos que u2= u1+ 2 = 2 + 2 = 4.
En esta actividad el usuario debe escribir una ecuación recursiva en la que un es igual a algún cálculo con un-1 (por ejemplo, un=un-1+2). El valor inicial u0 también debe estar especificado y ajustado por el usuario según su papel en el gráfico de la ecuación. Esta actividad utiliza las primeras 10 iteraciones de las ecuaciones para calcular los puntos de la gráfica. Estos puntos se conectan y así el estudiante puede identificar la tendencia global de cada gráfica. El usuario puede volver a la gráfica de cada ecuación y ver el valor de cada punto sobre ella,
Cuando pensamos en una ecuación, generalmente pensamos en algo como y=2x. Se da un valor a x y se recibe un valor único de y. En este caso, para obtener un valor no es necesario haber calculado un valor previo. Pero la situación es diferente en las ecuaciones recursivas. Una relación recursiva significa que cada valor de la función está determinando por el valor previo, excepto el valor inicial que debe ser estipulado, para con él determinar el primer valor. A continuación ese primer valor se utiliza en la ecuación para obtener el segundo valor y así sucesivamente.Este proceso se repite hasta llegar al número de iteraciones que hayan sido especificadas.
Por ejemplo, usemos la ecuación recursiva un = un-1 + 2. Debemos especificar también el valor inicial, que tomaremos como u0=0. Comparemos estos resultados con los de la función f(x) = 2x:
| u n = u n-1 + 2 | f(x) = 2 * x | |||
|
|
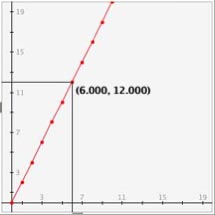
Observe que esta gráfica es semejante a la de la función f(x)=2x. Remplazando a x por valores enteros de 0 a 6 en la función f(x)=2x se obtienen exactamente los valores de la ecuación recursiva un = un-1 + 2. ¿Por qué esto es así? Veamos los valores de la 6a. posición sobre la gráfica. Para la función: f(6)=2x6=12. Recuerde que la ecuación recursiva es
un = un-1 + 2. Entonces u6 = u5 + 2. Pero, ¿cuál es el valor de u5? Sabemos que u5= u4 +2. Por lo tanto u6 = (u4 + 2) + 2. Y u4= u3 + 2. Entonces u6 = ((u3+ 2) + 2) + 2. Pero u3 = u2+2. En consecuencia, u6 = (((u2+ 2) + 2) + 2)+2. Igualmente, u2=u1+ 2 y entonces,
u6 = ((((u1+ 2) + 2) + 2)+2)+2. Finalmente, u1=u0+2=0+2=2. Por lo tanto, podemos calcular el valor u6 = (((((((0 + 2) + 2) + 2)+2)+2)+2) = 12. Estamos sumando 2, seis veces. Esto es lo mismo que 2x6, que es el valor de la función para x= seis veces. Hay pues una relación directa entre la función lineal y la función recursiva.
Es importante entender las ecuaciones recursivas porque se presentan en muchas situaciones de la vida diaria. Muchos de estos casos involucran ecuaciones recursivas más complicadas que la que acabamos de investigar. La función no recursiva no siempre es tan fácil de deducir.
Una ecuación recursiva frecuente es la relativa a interés compuesto. Veamos un ejemplo. Sara coloca inicialmente $1000000 en una cuenta de ahorros que le paga 3% de interés anual. Esto significa que en cada nuevo año debe recibir un 3% adicional a lo que tenía en el año inmediatamente anterior, situación que se puede representar con la fórmula
un = un-1 * (1 + 0.03), con u0= 1000000. El número de iteraciones sería el número de años que tuviera su dinero en esta cuenta de ahorros.
Esta actividad gráfica puede usarse con ejemplos de la vida real tales como interés compuesto y también con toda clase de ecuaciones recursivas. Puesto que la actividad crea una gráfica, el usuario es ahora capaz de comparar las ecuaciones con ecuaciones que le son más familiares. Más aún, podrá conectar las ideas abstractas de recursión con un gráfico visual concreto.
Recursos para la clase
- Actividad Generador de la curva de Hilbert
- Actividad Copo de nieve de Koch
- Actividad Crear Sucesiones
- Actividad Tapete de Sierpinski
- Actividad Triángulo de Sierpinski
- Discusión sobre Propiedades de los fractales
- Discusión sobre Recursión
- Taller Preguntas de exploración sobre Recursión
- Taller Preguntas de exploración sobre Recursión (doc).
Actividad
¿Cómo puedo utilizar esta actividad?
Descripción
Esta actividad permite graficar funciones recursivas. El estudiante especifica el valor inicial y la función recursiva hasta para tres ecuaciones. Se utilizan las 10 primeras iteraciones de las ecuaciones, para dibujar los resultados como puntos para una gráfica. El usuario puede volver sobre cada ecuación para ver los valores del punto graficado.
Controles y Resultados
Para la página de ecuaciones:
- El usuario puede ingresar hasta tres ecuaciones a esta página. Se hará referencia a ellas como "Relaciones"
- Cada ecuación tiene su propia variable. Hay una letra predeterminada y un valor inicial para cada variable. Si el usuario quiere cambiar la letra debe escribir una en la caja de texto junto al botón Establecer la variable. También puede cambiar el valor inicial de la variable escribiendo un número junto al u0 =. A continuación se debe hacer click en el botón Establecer la variable, para cambiar cada aparición de la letra en toda la relación.

Observe que en toda ecuación recursiva válida, debe usarse la misma letra en la ecuación. Entonces, si en un caso la variable es la letra a, la ecuación debe permanecer consistente, como en el ejemplo siguiente:El usuario debe ingresar una ecuación en la caja de texto que hay junto a los símbolos u n = . El valor de un depende del último valor de la variable (u n-1 ).
-
- Para obtener textos con con subíndice simplemente se digita la variable dependiente y luego n-1. La actividad está programada para escribir n-1 como subíndice.Tan pronto como la relación incluye una cadena de la forma un-1 (o cualquiera otra variable escogida por el usuario), se convierte en una ecuación recursiva valida,
- Cuando se hace click en el botón Borrar ecuación se borran la ecuación escrita en la caja de texto y la ecuación que aparece en el campo de texto.
-
- Tan pronto como el usuario está satisfecho con las variables y ecuaciones para cada relación, puede hacer click en el botón ¡Grafíquela! situado en la parte superior de la pagina, para ver las gráficas de las ecuaciones.
Para la página de gráficas:
-
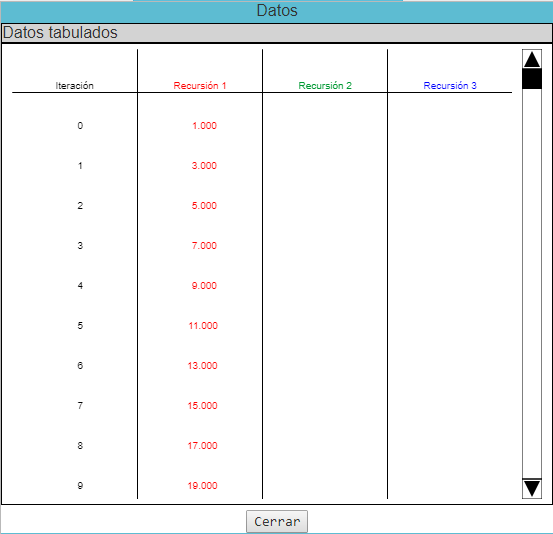
Para ver todos los valores de los puntos a la vez, haga click en el botón Mostrar datos. Entonces aparece un gráfico en ventana separada, en la que se listan todos los puntos.
-
-
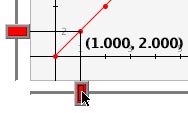
Para navegar sobre la gráfica, utilice las barras deslizadoras que hay debajo y a la izquierda de ella. Haga click en el rectángulo central y arrastre: a izquierda y derecha con la barra horizontal y hacia arriba y abajo con la barra vertical. Observe que ambas barras se mueven y que identifican el punto más cercano a ellas. El valor que aparece en la pantalla corresponde al punto al cual está unida la barra deslizadora en ese momento.
-
-
El usuario puede cambiar entre ecuaciones y por lo tanto puede ver sus valores a la vez. Puede hacerlo utilizando el menú desplegable que aparece debajo de la gráfica

- El usuario puede también cambiar la manera en que quiere que se desplieguen las gráficas. Si chequea la casilla Conectar los puntos estos serán unidos con una línea. Los puntos se conectan por defecto (es decir si no se chequea la casilla), para que se aprecie mejor la forma de la gráfica. Si se chequea la casilla Ajustar el tamaño del gráfico a los puntos el tamaño del gráfico se modificará de tal forma que se ajuste a todos los puntos.

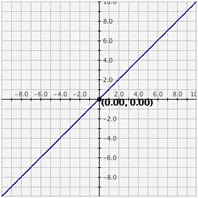
- Hay tres opciones para cuadrículas: Sin cuadrícula, Cuadrícula de líneas claras y Cuadrícula de líneas oscuras. Para activar cualquiera de estas opciones resalte el círculo correspondiente.

Gráfica sin cuadrícula Gráfica cuadrícula línea clara
:Gráfica cuadrícula línea oscura 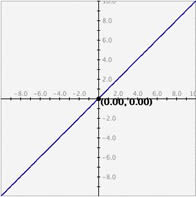
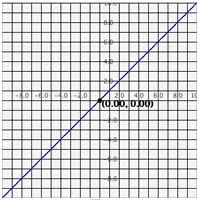
Hay dos formas de modificar el rango de los ejes.
1. Estableciendo valores exactos para los valores máx y min de los ejes. Puede establecer las fronteras de la gráfica haciendo click en en el botón Preferencias e ingresando los nuevos valores para x max, x min, y max, y min y/o iteraciones. A continuación haga click en el botón Establecer ventana para determinar las fronteras. Para volver a los valores predeterminados, haga click en el botón Valores predeterminados y en botón Establecer ventana, otra vez. Si no quiere cambiar los valores, debe hacer click en Cancelar.-

- Botones de Zoom/Desplazamiento: En la esquina superior derecha hay tres botones con imágenes de lupas.De arriba hacia abajo ellas representan: zoom in (acercamiento), zoom out (alejamiento, disminución) y desplazamiento, respectivamente.
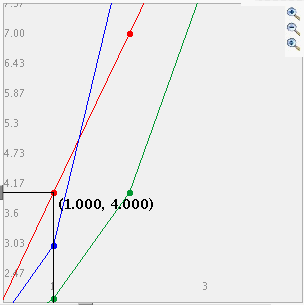
- Para un zoom de acercamiento haga click en el botón superior para activarlo y después haga click y arrastre sobre el área de la gráfica que se quiere magnificar. Las imágenes siguientes muestran primero el proceso de arrastrar con el ratón una caja alrededor de un área (izquierda) y después la imagen ampliada cuando se libera el botón del ratón (derecha). Observe que despues de que se ha ejecutado el acercamiento, el botón de la parte superior derecha ya no se ve activado.
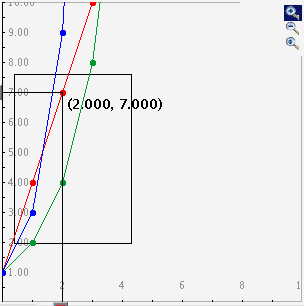 _
_
- Para disminuir el zoom, simplemente active el segundo de los tres botones. La gráfica se disminuirá automáticamente al duplicarse los valores máximo y mínimo de los ejes.
- Para usar la funcion de desplazamiento, haga click en el tercer boton para activarlo. Haga click y arrastre sobre la gráfica y se obtendrá el desplazamiento conforme al movimiento del mouse. Al soltar el mouse se libera también este botón...
- Para un zoom de acercamiento haga click en el botón superior para activarlo y después haga click y arrastre sobre el área de la gráfica que se quiere magnificar. Las imágenes siguientes muestran primero el proceso de arrastrar con el ratón una caja alrededor de un área (izquierda) y después la imagen ampliada cuando se libera el botón del ratón (derecha). Observe que despues de que se ha ejecutado el acercamiento, el botón de la parte superior derecha ya no se ve activado.
-
- En cualquier momento el usuario puede volver atrás y cambiar las ecuaciones recursivas, haciendo click en el botón de Retroceso.
Recursos y contexto curricular
Esta actividad permite explorar diferentes ecuaciones recursivas. La actividad puede trabajarse en grupos pequeños de 2-3 estudiantes durante unos 40 minutos si se utilizan las preguntantas de exploración y durante unos 20 minutos en caso contrario.
Ubicación en el currículo de matemáticas
Esta actividad puede usarse para:
- Enseñar a los estudiantes el tema de ecuaciones recursivas
- Mostrar hasta tres ecuaciones recursivas en una gráfica.
- Rastrear (identificar) valores individuales de una ecuación recursiva usando una gráfica.
Estándares alcanzados
Grados 9-12
- Algebra
- Analizar el cambio en varios contextos
- Representar y analizar situaciones matemáticas y estructuras utilizando símbolos algebraicos.
- Comprender patrones, relaciones y funciones
- Utilizar modelos matemáticos para representar y comprender relaciones cuantitativas,
- Números y operaciones
- Comprender los significados de las operaciones y cómo se relacionan entre ellas.
Esté preparado para:
- Proporcionar a los estudiantes varias ecuaciones recursivas para que las trabajen, por ejemplo experimentar con multiplicaciones y divisiones.
- Animar a los estudiantes para que ensayen con diferentes valores iniciales
- Conectar ecuaciones recursivas con ejemplos de la vida real, como interés compuesto.
- Mostrar a los estudiantes cómo leer la gráfica, rastrear los valores de la ecuación recursiva en cada punto y cambiar entre una ecuación y la siguiente.
Recursos para clases
- Actividad Generador de la curva de Hilbert
- Actividad Copo de nieve de Koch
- Actividad Crear Sucesiones
- Actividad Tapete de Sierpinski
- Actividad Triángulo de Sierpinski
- Discusión sobre Propiedades de los fractales
- Discusión sobre Recursión
- Lección Introducción a las sucesiones aritméticas y geométricas
- Lección Introducción a los fractales: infinito, auto similaridad y recursión
- Lección Propiedades de los fractales
- Taller Preguntas de exploración sobre Recursión
- Taller Preguntas de exploración sobre Recursión (doc).