Inicio Actividades Cálculo Grafíquelo paramétrico
Grafíquelo paramétrico
Temas
Grafíquelo paramétrico
¿En qué consiste la actividad Grafíquelo paramétrico ?
Esta actividad permite graficar pares ordenados y ecuaciones paramétricas en un mismo plano coordenado. La aplicación es similar a Grafíquelo, excepto que se ingresa la representación paramétrica de una función en lugar de la representación usual.
Las ecuaciones paramétricas son una forma de representar funciones y otras gráficas utilizando ecuaciones separadas para cada coordenada. El propósito es dar una dirección u orientacion a un objeto teórico que se desplaza a lo largo de una curva. En lugar de tener una función en la que y depende de x, hay dos ecuaciones x(t) and y(t) que dependen ambas de t. La variable t se llama el parámetro y las dos ecuaciones para x y para y se llaman las ecuaciones paramétricas. Los puntos sobre la gráfica tienen coordenadas (x(t), y(t)) para algún rango de valores de t.
Las ecuaciones paramétricas tienen la habilidad de producir gráficas que no pasarían la prueba de la recta vertical para funciones. Las funciones se pueden representar fácilmente con ecuaciones paramétricas, pero no todo conjunto de ecuaciones paramétricas puede ser representado por funciones. La siguiente es la gráfica de y=.5x^3 representada por las ecuaciones paramétricas x(t)=t and y(t)=.5t^3.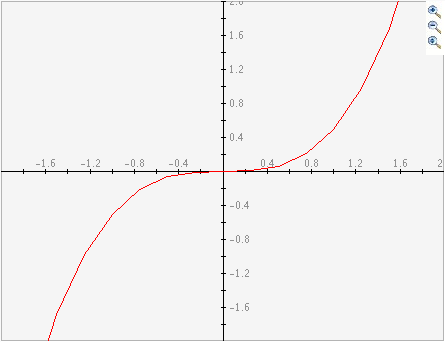
Para representar una función con sus ecuaciones paramétricas, simplemente haga x(t)=t and y(t)= la función original.
La siguiente es la gráfica de las ecuaciones paramétricas x(t)=sin(t) y y(t)=.5t^2. Esta gráfica no puede representarse con una función porque no satisface la prueba de la recta vertical 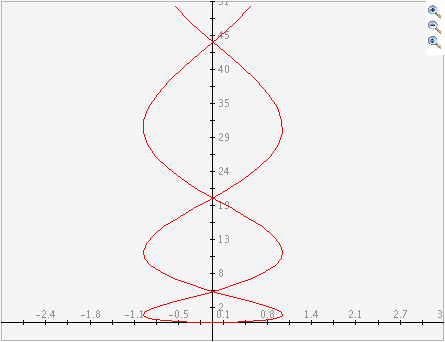
Recursos para la clase
- Actividad ¡Grafíquelo!
- Actividad Prueba de la recta vertical
- Discusión sobre Las funciones y la prueba de la recta vertical
- Taller Grafiquelo paramétrico. Preguntas de exploración
- Taller Grafiquelo paramétrico. Preguntas de exploración (doc)
Actividad
¿Cómo puedo utilizar esta actividad?
Descripción
Esta actividad permite graficar pares ordenados y ecuaciones paramétricas en un mismo plano coordenado.
Controles y Resultados
- La gráfica se muestra en la parte superior de la pantalla
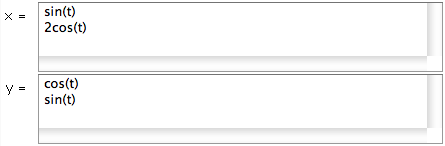
- El área Ecuación es para escribir las ecuaciones para x y para y. Para graficar ecuaciones paramétricas, escriba las ecuaciones par x y para y en los campos de texto junto a x= y y= respectivamente. Asegúrese de que las ecuaciones son funciones de t, puesto que las ecuaciones paramétricas se grafican con respecto al tiempo. Se pueden graficar hasta cuatro ecuaciones en el mismo diagrama. Ingrese una fórmula por línea, como se muestra.
- Las funciones básicas y sus composiciones se escriben como sigue:
Función Símbolo Ejemplos(incluyendo combinación de funciones suma
+
x + 3 x más tres
resta - 5 - t cinco menos t multiplicación * (t - 2)*t t por t menos 2 división / 3/t tres dividido por t potencia ^ t^3 - 1 t a la potencia 3, menos 1 potencia ** t**3 - 1 t a la potencia 3, menos 1 (pi) pi sin(pi*t) seno de (pi por t) raíz cuadrada sqrt(...) sqrt(t-1) raíz cuadrada de t menos 1 raíz n-sima
t^(1/n) t^(1/3) ráiz cúbica de t valor absoluto abs(...) abs(3 - t) valor absoluto de 3 menos t e a la potencia t exp(...) exp(t) e a la potencia t seno sin(...) sin(t**2) seno de t cuadrado coseno cos(...) cos(5 - t) coseno de 5 menos t tangente tan(...) tan(t) tangente t arcoseno asin(...) 2*asin(t) 2 por arcoseno t arcocoseno acos(...) acos(t) arcocoseno t arcotangente atan(...) atan(t) arcotangente t seno hiperbólico sinh(...) sinh(1 - t) seno hiperbólico de 1 menos t coseno hiperbólico cosh(...) cosh(10/t) coseno hiperbólico de 10 dividido por t tangente hiperbólica tanh(...) tanh(t) tangente hiperbólica de t logaritmo natural ln(...) ln(t) logaritmo natural de t logaritmo en base 10 log(...) log(t + 5) logaritmo en base 10 de t más 5 - Los datos se ingresan en el área Datos. Los puntos deben estar en la forma (x,y). Los valores de x y y pueden separarse con un espacio, pero esto no es necesario. Se requiere un retorno (enter) para separar un punto de otro. Después de ingresar las coordenadas, presione el botón Graficar/Actualizar para graficarlas.
- Si tiene dificultades copiando los datos desde la aplicación y pegándolos en una hoja de Excel, consulte la Ayuda para Copiar/Pegar de Excel
- Puede graficar un total de cuatro pares de ecuaciones de una vez y hasta un total de doce conjuntos de datos de una vez. Separe cada función con una coma o escríbala en una nueva línea. Separe cada conjunto de puntos escribiendo la palabra newgraph en una línea en la ventana Datos También puede especificar el color de sus gráficos remplazando la palabra newgraph con las siguientes palabras: bluegraph (gráfica azul) ,redgraph (roja) , greengraph (verde), blackgraph (negra),graygraph (gris) magentagraph (magenta), browngraph (café), cyangraph (gráfica cian). orangegraph (naranja) , purplegraph (púrpura), crimsongraph (carmesí), darkbluegraph (azul oscura).
- Usted puede elegir entre dos clases de gráficas. "Conectada" dibuja un segmento de recta desde un punto hasta el siguiente.. "Dispersa" dibuja los puntos como puntos físicos sobre la gráfica.Estas opciones no afectan la forma como se grafican las ecuaciones.

Dado que las ecuaciones paramétricas son funciones del tiempo, usted puede ajustar los tiempos inicial y final y también el intervalo. Para hacerlo, ajuste los valores en t Mínimo, t Máximo, e Intervalo t

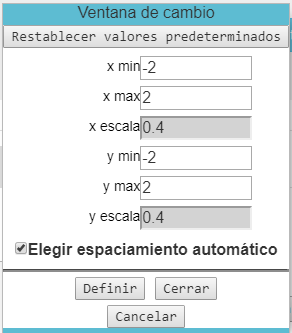
- Use el botón Definir Ventana para establecer como aparecerá el plano coordenado en su pantalla. Aparecerá una nueva ventana que le permite cambiar la configuración. X min and X max son los valores máximo y mínimo de x en la gráfica. Igualmente, Y mín and Y máx son los valores mínimo y máximo de y. Escala X y Escala Y son las distanciaa entre líneas verticales y lineas horizontales de la cuadrícula. Si usted optó por Elegir espaciamiento automático. el programa determinará una escala razonable, pero si no lo hizo puede seleccionar su propio espaciamiento. En el momento en que quiera restablecer la ventana de valores predeterminados seleccione el botón correspondiente: Restablecer valores predeterminados. Haga click en Definir para que los cambios hechos en los parámetros de la ventana tengan efecto.
- Usted puede escoger lo que quiere ver en la gráfica. Puede seleccionar mostrar todas las funciones, todos los datos y las líneas de cuadrícula, eligiendo la opción correspondiente, entre las siguientes del cuadro Mostrar

- La aplicación puede mostrarle la posición de cualquier Click. Sencillamente, haga click con el ratón en cualquier parte de la gráfica para conocer las coordenadas y estas aparecerán en el campo de texto Posición del ratón.

- Botones Zoom/Desplazamiento. En la esquina superior derecha del gráfico hay tres botones con imágenes de lupas. De arriba a abajo, representan acercamiento, alejamiento y desplazamiento, respectivamente.
- Para un zoom de acercamiento haga click en el botón superior para activarlo y después haga click y arrastre sobre el área de la gráfica que se quiere magnificar..Observe que despues de hacer click y arrastrar sobre el área seleccionada el botón ya no se ve seleccionado.
- Para disminuir el zoom, simplemente active el botón del medio. La gráfica se disminuirá automáticamente al duplicarse los valores máximo y mínimo de los ejes.
- Para usar la funcion de desplazamiento, haga click en el tercer boton para activarlo. Haga click y arrastre sobre la gráfica y se obtendrá el desplazamiento conforme al movimiento del ratón. Al aflojar la presión sobre el ratón se libera también el botón de desplazamiento.
- Seleccionando Espaciamiento automático se obtiene la menor ventana posible tal que todos los datos (puntos) caben en el plano coordenado. Tenga en cuenta que debe haber datos para que esta opción funcione.
- Para un zoom de acercamiento haga click en el botón superior para activarlo y después haga click y arrastre sobre el área de la gráfica que se quiere magnificar..Observe que despues de hacer click y arrastrar sobre el área seleccionada el botón ya no se ve seleccionado.
- Para ver una tabla de valores correspondiente a la función graficada selecciones el botón Mostrar tabla de datos. .
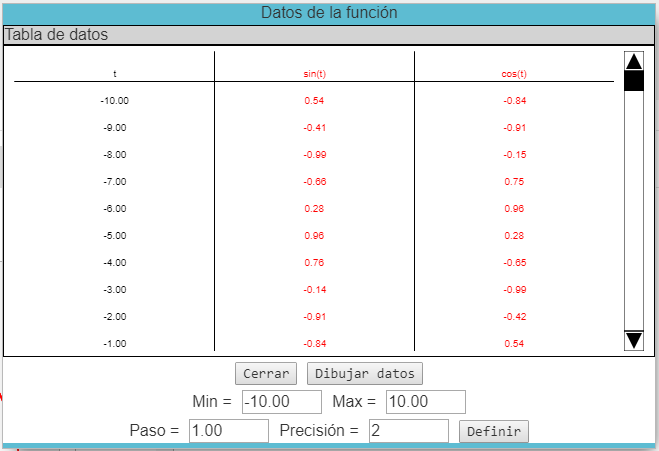
Los valores de t de la tabla se incrementan uniformemente y producen los correspondientes valores x(t) y y(t) para cada función graficada. Usted puede cambiar estos valores definiendo valores nuevos para t mín., t máx. y tamaño del incremento. Si ingresa un tamaño de incremento que no divide exactamente al rango, la tabla se detendrá en el mayor múltiplo del tamaño del incremento que sea menor que el máximo t. El campo precisión permite ajustar el número de cifras decimales que se muestran.
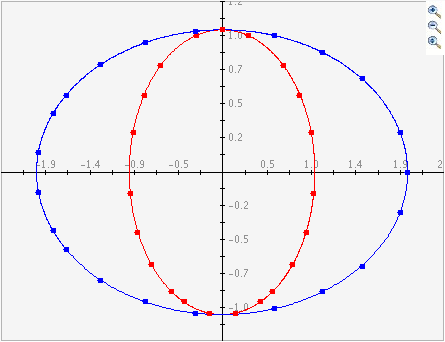
- Cuando se usa el boton Graficar Datos de la ventana Mostrar tabla de datos, los datos que figuran en la Tabla de datos se representan en la pantalla principal.
Recursos y contexto curricular
Esta actividad le permite al usuario graficar conjuntos de ecuaciones paramétricas y representar puntos en la misma ventana. La actividad es similar a Grafíquelo excepto porque los datos de entrada son ecuaciones paramétricas de la variable t.
Ubicación en el currículo de matemáticas
Esta actividad puede usarse para:
- Iniciar a los estudiantes en el tema de ecuaciones paramétricas
- Practicar las destrezas para graficar
- Ilustrar la relación entre funciones y ecuaciones paramétricas
- Evaluar expresiones algebraicas
- Determinar si una gráfica dada representa o no una función.
Estándares alcanzados
Grados 8-12
- Cálculo
- Los estudiantes encuentran las derivadas de funciones definidas paramétricamente y usan derivación implícita en una amplia variedad de problemas en fisica, química, economía, etc.
- Análisis matemático
- Los estudiantes demuestran comprensión de funciones y ecuaciones definidas paramétricamente y pueden graficarlas.
Esté preparado para:
- Definir parámetro y ecuación paramétrica
- Discutir y ejemplificar la prueba de la recta vertical
- Evaluar composiciones de funciones
- Explicar dirección y orientación
Recursos para clases
- Actividad ¡Grafíquelo!
- Actividad Prueba de la recta vertical
- Discusión sobre Las funciones y la prueba de la recta vertical
- Taller Grafiquelo paramétrico. Preguntas de exploración
- Taller Grafiquelo paramétrico. Preguntas de exploración (doc)
