Inicio Discusiones Cálculo Graficar funciones en el sistema de coordenadas polares
Discusiones
Graficar funciones en el sistema de coordenadas polares
Mentor: Ya discutimos sobre graficar puntos en el plano de coordenadas polares. Bueno, así como podemos graficar funciones en el plano Cartesiano, podemos graficar funciones en el plano de coordenadas polares.
Estudiante: ¿Cómo se ve una ecuación en coordenadas polares?
Mentor: En el sistema Cartesiano, generalmente x es la variable independiente y y es la variable dependiente. En el sistema de coordenadas polares, theta, simbólicamente θ, generalmente es la variable independientes y r es la variable dependiente.
Estudiante:¿No es como al revés del sistema Cartesiano? Quiero decir, en coordenadas polares se cita primero la variable dependiente y en el sistema Cartesiano la variable dependiiente es la segunda del par ordenado.
Mentor: Buena observación. Definitivamente es algo para tener en cuenta. ¿Por qué no tratamos de graficar una ecuación bien simple en la que la variable dependiente, r, es constante, Digamos r=3. La gráfica sería una circunferencia con radio de 3 unidades, ¿Sabes por qué?
Estudiante: ¡Sí, claro! Es así, porque r representa el radio. Y si r es 3 para todos los valores del ángulo, entonces se tiene que formar una circunferencia.
Mentor: ¿Y con qué ecuación crees que se crearía una recta?
Estudiante: Si un valor constante de r crea una circunferencia, entonces yo creo que un valor constante de theta daría una recta. ¿Sería θ=π/6 una recta?
Mentor: Sí, buen trabajo. Ahora consideremos una ecuación que sí tiene en ella la variable independiente, θ, digamos r=sin(θ). ¿Qué harías para graficar esta ecuación?
Estudiante: Bueno, necesitaría encontrar r para varias medidas de ángulos, ¿no? Podría hacer una tabla, elegir valores de θ para evaluar y remplazar θ por esos valores en la función para hallar mis pares de coordenadas. Entonces podría representarlos en una gráfica en polares.
Mentor: ¡Exacto!. Hay muchos tipos diferentes de ecuaciones que generan formas hermosas. Una función como r=2+(3*sin(θ)) se llama un limaçon (se pronuncia "limazón") o caracol. ¿Cómo la graficarias?
Estudiante: Bueno, también empezaría creando una tabla de valores para θ. Luego uso estos valores de θ en la función para hallar los valores de r. Mi tabla se vería así:
| θ | r=2+3*sin(θ) |
|---|---|
| 0 | 2 |
| π/6 | 3.5 |
| π/4 | 4.12 |
| π/3 | 4.60 |
| π/2 | 5.00 |
| 2π/3 | 4.60 |
| 3π/4 | 4.12 |
| 5π/6 | 3.5 |
| π | 2.00 |
| 7π/6 | .5 |
| 5π/4 | -.12 |
| 4π/3 | -.6 |
| 3π/2 | -1.00 |
| 5π/3 | -.60 |
| 7π/4 | -.12 |
| 11π/6 | .5 |
| 2π | 2.00 |
Estudiante: Entonces representaría los puntos en una gráfica polar, Los puntos graficados se verían así:
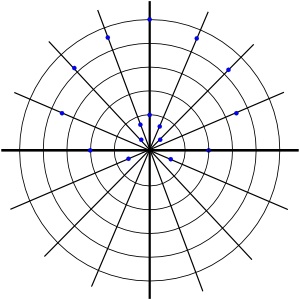
Estudiante: Pero conectar estos puntos parece complicado. ¿Y si omitiera algunos valores importantes en mi tabla?
Mentor: Esa es una muy buena observación. Y es la razón por la que a menudo preferimos usar computadores dado que ellos pueden calcular muchos más puntos mucho más rápidamente que nosotros. Trata de graficar esta función usando la actividad Coordenadas Polares y observa qué te resulta.
Estudiante: ¡Uao! ¡Es una gráfica muy bonita!
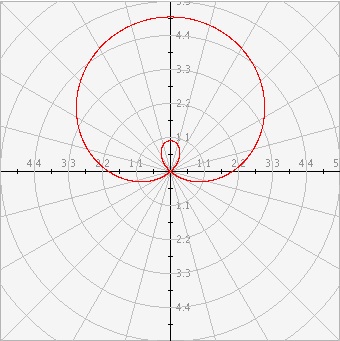
Mentor: Buen trabajo. Una ecuación de la forma a ± b*sin(θ) o a ± b*cos(θ) generar un limaçon. Practica un poco más. Aún ecuaciones tan sencillas como sin(a*θ) o cos(a*θ resultan interesantes. Juega con los valores de a y b, y mira qué pasa. Hay gráficas muy interesantes que resultan de graficar funciones trigonométricas en el sistema de coordenadas polares.
Nice work. Any equation of the form of the formula a ± b*sin(θ) or a ± b*cos(θ) will create a limacon. Try a few more. Even simple equations like sin(a*θ) or cos(a*θ) can be interesting. Play with the values of a and see what happens. There are many interesting graphs you can make by plotting trigonometric functions in the polar coordinate system!
