Mentor: Probablemente estás familiarizado con el sistema de coordenadas Cartesianas, que te permite graficar puntos y funciones en el plano coordenado. Si se te da un conjunto de puntos en la forma (x, y) deberías poder graficarlos en los ejes x, y de una gráfica.

Estudiante: Sí. Si me dieran el punto (2,3), empezaría en el origen e iría dos unidades hacia la derecha en el eje x;  y a continuación movería hacia arriba 3 unidades en la dirección de y.

Mentor: Es correcto.  Y si se te diera una función, digamos y=2x+3, probablemente también podrías graficarla.

Estudiante: Claro. Escogería valores de x que pudiera utilizar en la función para obtener valores de y. Entonces representaría esos puntos en la gráfica.

Mentor: ¡Exacto!  ¿Sabias que puedes graficar puntos en otro tipo de gráfica basada en el sistema de Coordenadas Polares? 

Estudiante: ¿Qué es el sistema de Coordenadas Polares?

Mentor: El sistema de coordenadas polares es un sistema circular en vez de un sistema de coordenadas rectangulares. Representas los puntos dados, en términos de un valor, r, que es la distancia desde el centro, y una medida angular que se da en grados, o más frecuentemente en radianes. ¿Recuerdas qué es un radián?

Estudiante: Seguro. Es otra unidad de medida de ángulos. Una circunferencia tiene 360 grados, que es lo mismo que 2π radiantes. pero, ¿para qué se usaría este sistema?

Mentor: Bueno, algunas veces es más apropiado describir una posición en términos de un movimiento circular, que en una línea recta. Este sistema es apropiado para funciones trigonométricas y se utiliza en navegación porque los valores pueden graficarse en términos de distancia (r) y dirección (ángulo, representado con la letra griega theta, de símbolo θ).

Estudiante: ¿Cómo se representan puntos en una gráfica polar?

Mentor: El sistema de coordenadas polares tiene un eje como en el sistema Cartesiano y un punto como el origen, llamado el polo. Tiene también un rayo que se extiende horizontalmente a través del polo, llamado el eje polar. El lugar de una cuadrícula, hay circunferencias concéntricas con centro en el polo que se hacen uniformemente más grandes y se irradian desde el polo. El plano de coordenadas polares se ve así: 

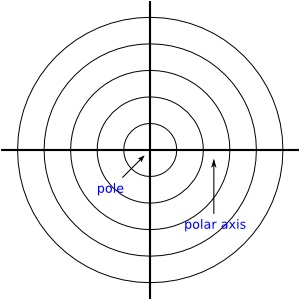
Mentor: Como las coordenadas rectangulares, también las coordenadas polares se designan con un par ordenado aunque los significados de los números son diferentes. El primer número del par, r, representa la distancia desde el polo y es como medir el radio de un círculo. El segundo número del par, θ, representa el valor del ángulo, medido desde el eje horizontal. El eje polar representa una medida angular de 0 radianes o 0 grados. Moviéndose en sentido contrario al giro de las manecillas de un reloj se genera un ángulo de medida positiva; en el sentido de las manecillas del reloj, la medida es negativa. 

Estudiante: Creo que voy entendiendo. En el sistema de coordenadas polares los ángulos se definen como en el círculo unitario, usualmente en radianes. Entonces, dadas las coordenadas polares (3, π/4), el punto está a tres unidades del centro, con un ángulo de π/4 radianes, medido en sentido contrario al giro del reloj desde el eje polar.

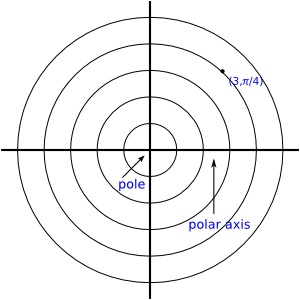
Estudiante: Entonces, ¿parece como si las coordenadas pudieran también ser negativas? 

Mentor: Es una excelente pregunta cuya respuesta es sí. Como en el círculo unitario, los ángulos negativos se miden desde el eje polar en el sentido del giro del reloj. ¿Recuerdas que -3π/4 es lo mismo que 5π/4?

Estudiante: Sí y ¿-4π/3 es  lo mismo que 2π/3?

Mentor: Correcto. Y, puesto que puedes sumar tantas rotaciones en la forma de múltiplos de 2π como quieras, cualquier ángulo puede tener una cantidad infinita de valores positivos y negativos. Además, r puede ser negativo. Un valor negativo de r indica que el punto está en el cuadrante opuesto del ángulo dado en el par coordenado. Por ejemplo, π/4  queda en el primer cuadrante, así que, con valores positivos de r  el punto se grafica a r unidades desde el polo en el primer cuadrante y con valores negativos de r se grafica en el cuadrante opuesto, el tercer cuadrante, sobre el ángulo identificado como 5π/4. ¿Dónde consideras que queda el punto      (-2, π/3) ?

Estudiante: Bueno, puesto que (2, π/3) se midió 2 unidades a la derecha a lo largo del eje polar, entonces -2 indicariá que el punto se mide 2 unidades a la izquierda a lo largo del eje polar y después  π/3 radianes en dirección opuesta la giro del reloj. Como el ángulo π/3 está en el primer cuadrante, entonces para graficar (-2, π/3) se graficaría un punto a dos unidades del polo a través de un ángulo 4π/3. ¿Cierto? 

Mentor: Cierto. Se vería así: 

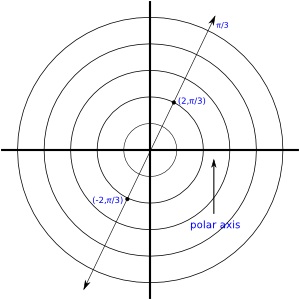
Estudiante:Entonces, ¿ un mismo punto puede tener diferentes valores?

Mentor: ¡Correcto! Los valores de r pueden ser positivos y negativos y θ  puede darse no solamente en valores positivos y negativos sino como cualquier valor θ + cualquier múltiplo de 2π. Entonces, a diferencia del sistema de coordenadas cartesianas, en el que cada punto tiene un único conjunto de coordenadas, en el sistema de coordenadas polares ¡cada punto puede tener un número infinito de coordenadas!

Estudiante: ¡Eso significa que el punto  (2,π/4) podría darse como  (2,-7π/4) o (2, 9π/4) o (-2,5π/4)!

Mentor: Exactamente. Representa esos puntos usando la actividad Coordenadas Polares y verifica que se trata del mismo punto.