Inicio Discusiones Trigonometría Elevando al cuadrado en el triángulo
Discusiones
Temas
Elevando al cuadrado en el triángulo
Mentor: Hoy trabajaremos con triángulos rectángulos. Antes de empezar, ¿puede alguno darme la definición de triángulo?
Estudiante: Es una figura de tres lados.
Mentor: Correcto. Ahora, sabiendo esto, ¿puedes decirme qué es un triángulo rectángulo ?
Estudiante: Un ángulo recto es un ángulo que tiene 90 grados, entonces un triángulo rectángulo ¿no sería un triángulo cuyos ángulos suman 90 grados?
Mentor: Estuviste bien al relacionarlo con un ángulo recto, pero no es que todos sus ángulos sumen 90 grados, sino que uno de los ángulos del triángulo mide 90 grados. Sería imposible que los ángulos sumaran 90 grados puesto que en todos los triángulos los ángulos deben sumar 180 grados.
Estudiante: OK, entonces un triángulo rectángulo es un triángulo que tiene un ángulo recto.
Mentor: Bien. Y ahora, sabiendo qué es un triángulo rectángulo, ¿cuál sería la suma de los otros dos ángulos?
Estudiante: Pues, si un triángulo tiene 180 grados y un ángulo recto tiene 90 grados, entonces la suma de los otros dos ángulos es igual a 90 grados.
Mentor: Perfecto. Ahora sabemos lo básico de un triángulo rectángulo. Hoy aprenderemos cómo encontrar la longitud del tercer lado de una triángulo rectángulo cuando se conocen las longitudes de los otros dos lados.
Estudiante: ¿Y por qué no se puede simplemente medir la longitud?
Mentor: Bueno, en algunos casos se puede, pero el proceso puede ser tedioso y se presta para errores humanos. El proceso matemático es mucho más seguro. Además, hay veces en las que no se puede medir, como cuando no tienes cerca una regla, o el triángulo no está dibujado a escala o sólo se dan números sin un dibujo que lo acompañe.
Estudiante: OK, entonces, si no es posible apoyarse en mediciones, ¿cómo hacerlo?
Mentor: Para encontrar lados desconocidos en triángulos rectángulos usamos lo que se conoce como Teorema de Pitágoras. Se llama así porque fue establecido por un filósofo y científico griego llamado Pitágoras.
Estudiante: ¿Cuál es el teorema de Pitágoras y como se usa?
Mentor: El teorema de Pitágoras establece que A 2 +B 2 =C 2 donde A representa un cateto del triángulo, B representa el otro cateto y C representa la hipotenusa, que es el lado opuesto al ángulo recto.
Estudiante: OK, pero, ¿cómo usamos este teorema, dado que involucra tres variables?
Mentor: Bueno, recuerda que al inicio de la lección dije que encontraríamos la longitud del tercer lado de un triángulo utilizando las longitudes de los otros dos lados.
Estudiante: ¡Ya lo recuerdo! Entonces, podemos remplazar dos de las tres variables con los lados que conocemos. Pero, ¿cómo sabemos qué longitudes representan las variables?
Mentor: Bueno, si designo los lados de mi triángulo con A, B y C donde A y B son los catetos del triángulo y C es la hipotenusa, ¿cómo ayudaría esta información cuando se use el teorema de Pitágoras?
Estudiante: Bueno, tendria sentido que A fuera la longitud del lado A y B fuera la longitud del lado B.
Mentor: Bien. Ahora veamos por qué y cómo trabaja este teorema y entonces podremos practicar usándolo un par de veces. Vamos a Cuadrado del triángulo.
Estudiante: Hay un triángulo con un cuadrado sobre cada lado, ¿es un triángulo rectángulo?
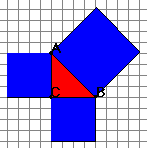
Mentor: Mira en la parte del lado en que dice medidas de ángulos ydime si es un triángulo rectángulo
Estudiante: ¡Sí es! El ángulo C es de 90 grados.
Mentor: Correcto, en esta actividad el triángulo siempre es un triángulo rectángulo.Usaremos esta actividad para verificar el teorema de Pitágoras.
Estudiante: Pero, espere un momento, los ángulos están etiquetados como A, B y C; yo pensaba que el teorema de Pitágoras tenía que ver con las longitudes de los lados.
Mentor: Tienes razón, el teorema de Pitágoras trabaja con las longitudes de los lados, pero recuerda que en situaciones diferentes las variables tienen diferentes significados. No importa cómo se designe el triángulo, A, B y C representarán siempre los lados.
Estudiante: Asi que en este caso sería (recta AC) 2 +(recta BC) 2 = (recta AB) 2 .
Mentor: Exactamente.
Estudiante: OK, entonces ¿para qué son los cuadrados pegados al triángulo? Yo pensaba que el teorema de Pitágoras sólo tenía que ver con triángulos.
Mentor: Tienes razón en cuanto el teorema de Pitágoras se utiliza solamente con triángulos, pero si ves los lados en el teorema de Pitágoras encontrarás que todos están elevados al cuadrado. Entonces, veamos lo que sucede realmente cuando elevas un número al cuadrado. Toma una hoja de papel cuadriculado y elevemos 4 al cuadrado
Estudiante: Eso es fácil, es 16.
Mentor: Correcto, pero veamos en primer lugar de dónde viene la expresión "elevar al cuadrado".
Estudiante: OK, ya tomé una hoja de papel cuadriculado, ¿qué hago?
Mentor: En primer lugar, sombrea cuatro casillas en fila.
Estudiante: ¿Es cuatro porque cuatro es el número que tratamos de elevar al cuadrado?
Mentor: Correcto, si estuviéramos tratando de elevar nueve al cuadrado entonces se sombrearían nueve casillas en fila. Ahora, tú sabes que cuatro elevado al cuadrado es cuatro veces cuatro, ¿verdad?
Estudiante: Sí, siempre es el número multiplicado por sí mismo.
Mentor: Así es, y ¿recuerdas que multiplicar es simplemente sumar números varias veces, y entonces 5*3 es de hecho 5+5+5?
Estudiante: Sí, y 2*5 sería 2+2+2+2+2.
Mentor: O más simplemente, podría ser 5+5, pero tienes la idea correcta. Entonces, ¿qué sería 4*4?
Estudiante: Bueno, sería 4+4+4+4, ¿no es así?
Mentor: Bien. Ahora, ya tenemos el primer 4 representado en el papel cuadriculado así que añadamos cuatro en la fila que está inmediatamente debajo del primer cuatro. Así tenemos 4+4. Añadamos otro 4 en la fila exactamente debajo del segundo 4 y obtenemos 4+4+4. ¿Adivinas que haremos en seguida?
Estudiante: ¡Añadir otro 4 debajo del anterior!
Mentor: Bien, y con todo lo que está sombreado, ¿qué tienes?
Estudiante: ¡Es un cuadrado!
Mentor: Correcto, de ahí viene la expresión elevar al cuadrado, porque el resultado es en efecto un cuadrado. Para afianzar la idea, trata de elevar tres al cuadrado.
Estudiante: ¡También da un cuadrado!
Mentor: Bien, entonces, ¿ya puedes adivinar por qué hay cuadrados pegados a los lados del triángulo en Elevando al cuadrado en el Triángulo?
Estudiante: Bueno, se llama elevando al cuadrado en el triángulo así que han elevado al cuadrado cada lado del triángulo.

Mentor: Pero, ¿por qué la actividad se llama Elevando al cuadrado en el triángulo? Piensa en el teorema de Pitágoras.
Estudiante: ¡Ah, claro! En el teorema de Pitágoras A, B y C se elevaron todos al cuadrado, y A, B, y C representan los lados del triángulo, así que elevaron al cuadrado los lados del triángulo,
Mentor: ¡Exactamente! Esta actividad se diseñó para ayudar en la comprensión del teorema de Pitágoras por eso muestra en un diagrama lo que realmente significa el teorema. Ahora, usando esos cuadrados ¿cómo puedes verificar si el teorema de Pitágoras es verdad?
Estudiante: Bueno...si A 2 +B 2 =C 2 no sería (el cuadrado sobre el lado A)+ (el cuadrado sobre el lado B)=(el cuadrado sobre el lado C)?
Mentor: Sí, pero ¿qué parte del cuadrado? ¿El perímetro?
Estudiante: Umm, no sé.
Mentor: Bien; volvamos al cuadrado que dibujaste en el papel cuadriculado. Antes de empezar dijiste que el cuadrado de 4 es 16, lo cual es verdad. Entonces, ¿el perímetro del cuadrado dibujado es 16?
Estudiante:Sí, sí es!
Mentor: Sólo para estar seguros. trata con el cuadrado que dibujaste para tres elevado al cuadrado. ¿Cuál es el perímetro de ese cuadrado?
Estudiante: Es 12...pero tres al cuadrado es 9.
Mentor: Correcto, esto significa que el hecho de que el perímetro del primer cuadrado fuera igual al cuadrado del lado fue una casualidad. La razón para esto fue que el cuadrado de cuatro es cuatro veces cuatro, que da el área, y la longitud del lado es 4 y hay cuatro lados así que la longitud del lado*4 es el perímetro. Ahora que sabemos que la respuesta no es el perímetro, ¿con qué ensayamos?
Estudiante: ¿Qué tal el área?
Mentor: OK, trata con tu cuadrado de cuatro por cuatro.
Estudiante: ¡Es 16! Pero verifiquemos con el cuadrado de tres por tres para estar seguros de que es correcto.
Mentor: Buena idea.
Estudiante: El área del cuadrado de tres por tres es nueve. ¡Funciona!
Mentor: OK, entonces hemos descubierto que el cuadrado de un número es igual al área de su cuadrado. Entonces, ¿qué podemos esperar ahora con respecto al teorema de Pitágoras?
Estudiante: Sería que (el área del cuadrado sobre el lado A) +(el área del cuadrado sobre el lado B)=(el área del cuadrado sobre el lado C).
Mentor: Perfecto. Entonces, si miras en el lado izquierdo de las imágenes en la región que dice "área" verás el área de los cuadrados. ¿Qué notas en relación con ellas?
Estudiante: Cuadrado AC+Cuadrado BC=Cuadrado AB.
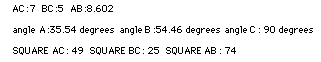
AC:7 BC: 5 AB:8.602
ángulo A:35.34 grados, ángulo B: 54.46 grados ángulo C: 90 grados
Cuadrado AC:49 Cuadrado BC: 25 Cuadrado AB: 74
Mentor: Como el área está designada con "área" puedes decir que todos los números en esa región son áreas. Entonces, ¿funciona el teorema de Pitágoras?
Estudiante:¡Sí!
Mentor: Ten cuidado. Hemos descubierto que utilizar sólo un resultado puede conducir a error. Trata cambiando las longitudes de los lados AC y BC usando los deslizadores en la parte inferior del diagrama, ¿se sigue cumpliendo?
Estudiante: ¡Sí! No encuentro ningún arreglo en el que no funcione.
Mentor: Bien, ahora que sabemos que el teorema de Pitágoras funciona y por qué lo hace, podemos resolver problemas utilizándolo. ¿Recuerdas qué dije sobre para qué se usa?
Estudiante: Para encontrar la longitud de un lado del triángulo cuando se conocen las longitudes de los otros dos lados.
Mentor: Estuviste cerca, pero esto no funciona con toda clase de triángulos. ¿Con cuáles funciona?
Estudiante: ¡Ah, claro! Sólo funciona con triángulos rectángulos.
Mentor: OK, entonces voy a darte las longitudes de dos lados y tú me dices cuál es la longitud del tercer lado, usando el teorema de Pitágoras. Es más fácil si usas una calculadora.
Estudiante: OK,Tengo calculadora. ¡Estoy listo!
Mentor: OK, empezaré dándote los dos catetos y tú debes hallar la hipotenusa. OK, un cateto es 5 y el otro es 7. ¿Cuál es la hipotenusa?
Estudiante: OK, entonces 5 2 es 25 y 7 2 is 49 y 25+49=74. ¡La hipotenusa es 74!
Mentor: No exactamente, recuerda que es A 2 +B 2 =C 2 . Hiciste bien la primera mitad A 2 +B 2 =C 2 pero cuando obtuviste 74 olvidaste que 74 es C 2 , no C. Entonces, ¿qué debes hacer para terminar de resolver este problema?
Estudiante: ¿74 al cuadrado?
Mentor: No, piensa en esto algebraicamente, 74=C 2 , ¿cómo encontrarías el valor de C?
Estudiante: ¡Sacas raíz cuadrada en ambos lados!
Mentor: Bien, entonces termina de resolver el problema.
Estudiante: OK, la raíz cuadrada de 74 is 8.6, por lo tanto C=8.6.
Mentor: ¡Muy bien! Ensayemos con otro. ¿Qué tal con catetos de 3 y 4?
Estudiante: OK, 3 2 es 9 and 4 2 es 16 asi que 9+16=25. Entonces la raíz cuadrada de 25 is 5!
Mentor: Buen trabajo. ¿Sientes que sabes cómo calcular la longitud de la hipotenusa cuando se dan las longitudes de los dos catetos?
Estudiante:¡Sí! ¿Qué sigue?
Mentor: Ahora trataremos de hallar la longitud del segundo cateto cuando se dan las longitudes del primer cateto y de la hipotenusa. Para hacerlo tenemos que aplicar un poco de álgebra. Puedes intentarlo primero y si tienes algún problema yo te ayudo. ¿Qué tal con 15 y 7?
Estudiante: ¿Cuál es la hipotenusa y cuál es el cateto?
Mentor: Bien, la hipotenusa es siempre el lado más largo en un triángulo rectángulo. Esto es así porque el lado más largo se opone al ángulo más grande, el segundo lado más largo se opone al al segundo ángulo más grande y el lado menor se opone al ángulo más pequeño. Sabemos que un triángulo tiene sólo 180 grados y que la hipotenusa tiene que ser el lado más largo porque lo más grande que puede ser un ángulo en un triángulo rectángulo, aparte del ángulo recto, es 89.999. En consecuencia, como el ángulo recto mide 90 grados y lo más que podría medir cualquier otro ángulo es 89.999 entonces el lado que se opone al ángulo recto tiene que ser el lado más largo, conocido como hipotenusa. A partir de esto, ¿me puedes decir cuál de 15 o 7 es la longitud de la hipotenusa?
Estudiante: Tiene que ser 15.
Mentor: Correcto, porque obviamente 15 es más que 7. ¿Ahora puedes hallar el otro cateto?
Estudiante: Bueno, sería 7 2 es 49 y 15 2 es 225. Por lo tanto 49+B 2 =225. ¿Saco la raíz cuadrada de 225?
Mentor: No, eso sería si ya tuviéramos los dos catetos; aquí es donde usamos el álgebra. ¿Cómo dejamos la B sola en un lado de la igualdad?
Estudiante: Pues, tendría que restar 49 de 225 lo cual da 176. ¿Entonces B es igual a 176?
Mentor: No, recuerda que la hipotenusa tiene que ser el lado más largo y la hipotenusa es 15, así que 176 es mucho más. Tienes que aplicar el álgebra para hallar B por tí mismo.
because remember the hypotenuse has to be the longest side, and the hypotenuse is 15, so 176 is way too much. You need to finish the algebra to get B all the way alone.
Estudiante: Bueno, entonces saco la raíz cuadrada de 176.
Mentor: Bien, y ¿cuál es la respuesta?
Estudiante: Es 13.266.
Mentor: Excelente trabajo. Ahora sabes qué es un triángulo rectángulo, qué es el teorema de Pitágoras, por qué funciona el teorema de Pitágoras y cómo resolver problemas usando el teorema de Pitágoras. ¿Tienes alguna pregunta?
Estudiante: Usted me dijo cómo hallar el tercer lado si tengo el primero y el segundo catetos, y cómo hallar el tercer lado si tengo la hipotenusa y el primer cateto, pero ¿cómo hago si tengo la hipotenusa y el segundo cateto?
Mentor: Se halla lo mismo que cuando se tienen la hipotenusa y el primer cateto. Las variables A y B son intercambiables siempre y cuando las mantengas constantes.
Estudiante: !Ya entiendo! Los catetos son la misma cosa, de tal manera que no es necesario tener estrategias distintas para encontrar cualquiera de ellos.
Mentor: Correcto. ¿Alguna otra pregunta?
Estudiante: ¡Nop!
