Inicio Actividades Estadística Distribución normal ajustada
Distribución normal ajustada
Temas
Distribución normal ajustada
¿En qué consiste la actividad Distribución normal ajustada ?
Esta aplicación permite experimentar con conjuntos de datos generados aleatoriamente para varios tamaños de muestra y desviaciones estándar.
En la gráfica, la curva de color negro y el cuadro de la Gaussiana original muestran los valores de la media esperada, la desviación estándar y la amplitud, para el conjunto de datos. Cuando se hace un experimento, la actividad genera números aleatorios que siguen esa distribución y los muestra en la misma gráfica. Dado que estos números están basados en la Gaussiana original, se espera que la nueva distribución sea similar a la distribución de base, pero, como los números son generados aleatoriamente, posiblemente la nueva distribución será ligeramente diferente.
En el mundo real, esta variabilidad es una cualidad ineludible de la naturaleza -los científicos muy rara vez tienen acceso a la "Gaussiana origina" y por lo tanto deben intentar averiguarla a partir solamente de sus muestras. Para hacerlo, frecuentemente hacen múltiples ensayos con muestras de gran tamaño para minimizar el efecto de la aleatoriedad. Por ejemplo, en esta simulación, la Gaussiana ajustada generalmente es más parecida a la Gaussiana original con una muestra de tamaño 10000 que con una muestra de tamaño 100.
Esta distribución fue generada con una muestra de tamaño 100. Como puede observar el grado de variabilidad es muy grande.
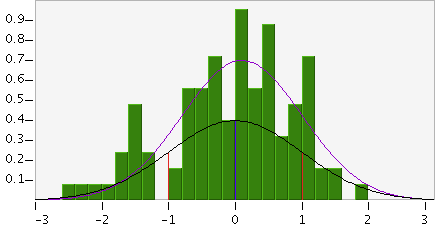
Sin embargo, la siguiente distribución fue generada usando una muestra de tamaño 1000. En este caso hay una variabilidad mucho menor.
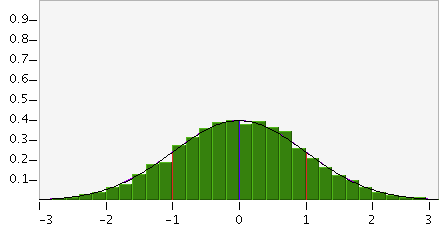
Es más, un cambio en la desviación estándar puede afectar la variabilidad de la muestra. Si la desviación estándar es grande, habrá más variabilidad tanto en los números individuales como en la Gaussiana ajustada como un todo.Esto significa que los científicos requerirán más experimentos y mayores tamaños de muestra, para hallar con precisión la Gaussiana ajustada para fenómenos del mundo real altamente variables.
Recursos para la clase
- Actividad Distribución normal
- Actividad Curvas Gaussianas superpuestas
- Actividad ¡Grafíquelo!
- Actividad Distribución sesgada
- Discusión sobre La curva de campana revisada
- Discusión sobre Promedio, mediana y moda
- Discusión sobre La distribución normal y la curva de campana
* Nota del traductor: La denominación "Campana de Gauss" es posiblemente más utilizada que "Curva de campana".
Actividad
¿Cómo puedo utilizar esta actividad?
Descripción
Esta actividad le permite al usuario experimentar con diferentes tamaños de intervalos de clase y número de ensayos, con los cuales crear una distribución normal.
Controles y Resultados
- La gráfica muestra los valores de los resultados de la distribución normal. La curva de color negro muestra el resultado esperado de los ensayos, con una media de cero, representada por la línea azul. Los círculos de color negro en la base de las lineas rojas muestran la desviación estándar. La curva de color púrpura muestra la distribución normal ajustada de los ensayos, que usualmente es similar a la distribución esperada.
- Para cambiar la desviación estándar seleccione y arrastre cualquiera de los círculos negros. Desplazarlos para quedar más cercanos disminuye la desviación estándar, mientras que separarlos la aumenta. La desviación estándar máxima es 1.250, mientras que la mínima es 0.410.
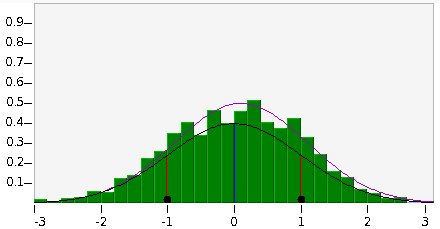
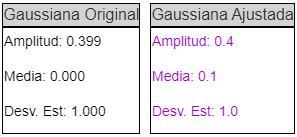
- En los cuadros siguientes se muestra información sobre la Gaussiana Original y la Gaussiana Ajustada. La amplitud de la distribución es el punto más alto en la gráfica. La media es el promedio de todos los resultados del ensayo. La desviación estándar mide la variabilidad de los resultados del ensayo. Típicamente, en las dos Gaussianas -la original y la ajustada-, estas tres medidas son muy similares.
- También puede cambiar las líneas de la cuadrícula de la gráfica seleccionando la opción en el cuadro Mostrar. Esto puede ayudarle a determinar la altura exacta de cada una de las barras de la gráfica.

- Para dibujar un histograma escoja en el menú desplegable el número de ensayos deseados. Puede cambiar la longitud del intervalo de clase utilizando la barra deslizante. Cuando cambia la configuración se genera automáticamente un nuevo histograma, pero si quiere generar otro histograma sin cambiar la configuración puede presionar "Crear nuevo histograma con".

Recursos y contexto curricular
Esta actividad le permite al usuario experimentar utilizando muestras aleatorias de varios tamaños para aproximar desviaciones estándar. Los estudiantes pueden usar esta aplicación para entender como la variabilidad de una muestra cambia con base tanto en el número de ensayos como en la desviación estándar de la distribución. Esta actividad es apropiada para trabajar en grupos de dos o cuatro estudiantes durante quince a veinte minutos.
Ubicación en el currículo de matemáticas
- reforzar la relación entre tamaño de muestra y exactitud de una muestra aleatoria
- reforzar la relación entre variabilidad de la muestra y exactitud de una muestra aleatoria
- demostrar la diferencia entre teórica (infinitos ensayos) y real (muestra grande o pequeña)
Estándares alcanzados
Grades 9-12
- Análisis de datos y Probabilidad
- Desarrollar y evaluar inferencias y predicciones basadas en datos
- Formular preguntas que pueden ser abordadas con datos y recogiendo, organizando y mostrando datos relevantes para responderlas.
- Seleccionar y utilizar métodos estadísticos apropiados para el análisis de datos.
Esté preparado para:
- responder la pregunta: "¿Por qué la Gaussiana ajustada es diferente de la Gaussiana original? "
- discutir tamaño de la muestra y sus efectos sobre el resultado de un experimento
- discutir desviación estándar y sus efectos sobre el resultado de un experimento
Recursos para clases
- Actividad Distribución normal
- Actividad Curvas Gaussianas superpuestas
- Actividad ¡Grafíquelo!
- Actividad Distribución sesgada
- Discusión sobre La curva de campana revisada
- Discusión sobre Promedio, mediana y moda
- Discusión sobre La distribución normal y la curva de campana
- Lección sobre Promedio, mediana y moda
- Lección sobre La curva de campana
