Curvas Gaussianas superpuestas

Las curvas Gaussianas se usan con frecuencia cuando se calculan las probabilidades de eventos aleatorios. Una clase especial de curva de Gauss es la distribución normal que es útil en probabilidad porque el área bajo la curva es igual a 1. Es frecuente que los cientificos encuentren conjuntos de datos que pueden representarse con curvas Gaussianas. Cuando se hacen mediciones continuas, como la altura de una planta, el peso de seres humanos, o el pH de una sustancia, los datos pueden representarse usualmente con un distribución de Gauss. Y a medidad que el número de datos crece, su representación se verá más y más como una curva Gaussiana. 

En el caso del peso de los seres humanos, si tomamos una muestra de hombres o mujeres de una cierta edad, habrá muchos pesos que rondan el peso promedio. Entonces, a medida que se consideran pesos alejados de ese promedio, podrá notarse que hay cada vez menos datos con dicho peso.

Esta actividad permite ver dos curvas Gaussianas en la misma ventana, para analizar la posibilidad de que haya diferencia en los dos conjuntos de datos. Si las áreas bajo las dos curvas ocupan un área similar entonces hay una razón estadística para pensar que realmente pueden tener la misma media, a pesar de una diferencia en la media experimental.

La pequeña diferencia en las medias examinadas puede deberse a la diferencia probabilidad teórica versus probabilidad experimental.  Cuando se toma una muestra aleatoria de la poblacion ella puede no reflejar los parámetros exactos de la población total. Esta aplicación puede usarse para determinar la probabilidad de que una muestra aleatoria sea realmente indicativa de su población. 

Descripción

Controles y Resultados

Controles deslizantes

• Puesto que las funciones ya están graficadas, usted puede manipular los coeficientes y las constantes de la función con los controles deslizantes. Esta manipulación incidirá en la gráfica en diferentes formas, dependiendo del color del control:
   
• • Control Púrpura:  Ajusta la amplitud o la altura de la curva. Entre más grande sea el valor del control púrpura, más alta será la función. Este valor debe ser siempre mayor que cero.
  • Control Rojo: Ajusta la desviación estándar o anchura de la curva. A medida que este valor crece, la gráfica se extenderá horizontalmente. Este valor dethe graph will appear to stretch out horizontally. Este valor debe ser siempre mayor que cero.
  • Control verde:  Ajusta la media o desplazamiento horizontal de la curva. A medida que ajusta este control la gráfica se deslizará horizontalmente. Esta variable puede tomar cualquier valor.
• Después de cambiar la función con los mencionados controles usted puede regresarlos a sus valores originales -los que tenía cuando ingresó la función-. presionando el botón Reiniciar deslizadores.
  
• Usted puede modificar el máximo, el mínimo y la longitud del incremento  de cada deslizador, de dos maneras: El botón Límites del deslizador produce un recuadro  de diálogo que permite fijar los valores máximo y mínimo de cada deslizador así como el incremento en el avance de  cada barra deslizadora. Este incremento determina con qué precisión puede usted controlar el valor de la constante. Por ejemplo, si fija el mínimo en 0, el máximo en 1 y el incremento en 0.1, al mover el deslizador la constante se incrementa de 0 a 0.1 a
  0.2 a 0.3, etc. Pero si lo fija en 0.2, al mover el deslizador la constante avanzará de 0 a 0.2 a 0.4, etc.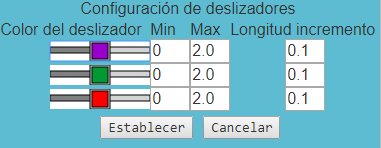
• 

• El número de incrementos debe ser menor que 200. Si ingresa parámetros tales que el número de incrementos es mayor que 200, le aparecerá un mensaje que le pide hacer un reajuste cambiando los valores máx, o mín del deslizador o la longitud del incremento.  

Deslizador negro

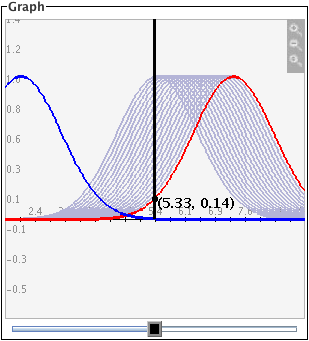
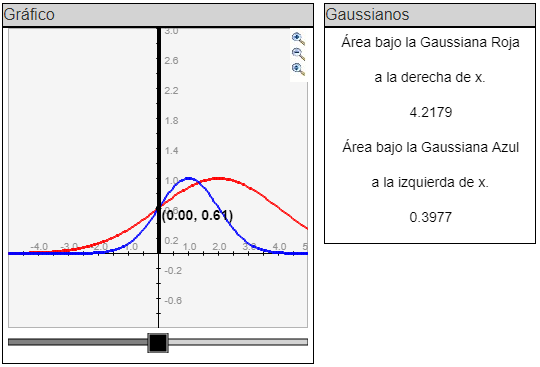
• El control deslizante de color negro fija una cota para las integrales de las dos curvas Gaussianas. Para la curva roja, el contro negro establece la cota o  límite inferior para la integral en tanto que el límite superior es infinito. Para la curva azul, el control establece la cota superior para la integral, mientras que el límite inferior es infinito negativo. Los resultados de estas integrales se muestran en el rectángulo llamado Gaussianas 
• 
  

Líneas de cuadrícula

• Hay tres clases de cuadrícula: Sin cuadrícula, Cuadrícula de líneas claras y Cuadrícula de líneas oscuras. Elija la opción correspondiene

Sin lineas de cuadrícula	Cuadrícula de líneas claras	Cuadrícula de líneas oscuras

Cambiar las escalas X y Y
Esta actividad permite cambiar el rango de los ejes de dos maneras: 

• Estableciendo valores exactos para los máximos y los mínimos de los ejes. Se pueden definir los límites de la gráfica haciendo click en en botón Definir Ventana e ingresando nuevos valores para máx x, mín x, máx y, o mín y. Tambíen puede fijar los incrementos en las escalas X y Y o dejar que la actividad escoja estos valores de manera automática. Haga click en el botón Definir Ventana, para establecer estos valores.
  Para volver a los valores predeterminados, haga click en el botón Usar  valores predefinidos y después presione el botón Establecer. Si no quiere cambiar la configuración de la ventana, presione Cancelar.
   
   
• En la esquina superior derecha del gráfico hay tres botones con imágenes de lupas. De arriba a abajo, representan acercamiento, alejamiento y desplazamiento, respectivamente. 
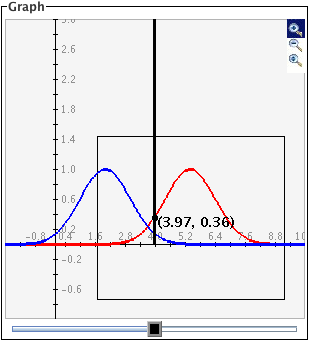
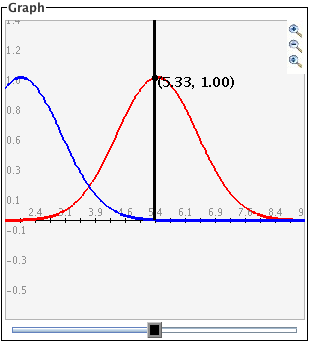
• Para un zoom de acercamiento haga click en el botón superior para activarlo y después haga click y arrastre sobre el área de la gráfica que se quiere magnificar. Las imágenes siguientes muestran primero el proceso de arrastrar con el ratón una caja alrededor de un área (izquierda) y después la imagen ampliada cuando se libera el botón del ratón (derecha). Observe que despues de que se ha ejecutado el acercamiento, el botón de la parte superior derecha ya no se ve seleccionado.
• • Para disminuir el zoom, simplemente active el segundo de los tres botones. La gráfica se disminuirá automáticamente al duplicarse los valores máximo y mínimo de los ejes.

  •  Para usar la funcion de desplazamiento, haga click en el tercer boton para activarlo. Haga click y arrastre sobre la gráfica y se obtendrá el desplazamiento conforme al movimiento del  ratón.  Al aflojar la presión sobre el ratón se libera también el botón de desplazamiento.

• Rastreo de funciones

• Seleccionando la opción Mostrar rastro permanecerán visibles las gráficas anteriores (en color gris claro), cuando cambie la función moviendo los deslizadores.  Para eliminar el rastro, haga click en el botón borrar rastro. Para detener el rastreo, deje sin selección el botón Mostrar rastro.   

La aplicación Gaussianas Superpuestas  permite cambiar los parámetros de dos curvas Gaussianas y entonces determinar si probablemente existe o  no diferencia entre los datos representados por las curvas. Esta actividad mide el área bajo las curvas Gaussianas, que es una herramienta utilizada para calcular probabilidades en datos distribuidos normalmente.   

Esta actividad está recomendada para trabajarse en grupos de dos o tres estudiantes durante veinticinco a treinta minutos si usted utiliza las preguntas de exploracion. 

• Calcular P-valores para curvas normales
• Enseñar a los estudiantes cómo el cambio de diferentes parámetros afecta una curva Gaussiana. 
• Enseñar a los estudiantes cómo el área bajo una curva Gaussiana se relaciona con probabilidad
• Introducir a los estudiantes en el tema de errores Tipo I y Tipo II

Grados  9-12

• Análisis de datos y probabilidad
  • Desarrollar y evaluar inferencias y predicciones basadas en datos
  • Formular preguntas que pueden ser abordadas con datos,  y recolectar, organizar y representar datos relevantes para responderlas. 
  • Seleccionar y usar métodos estadísticos apropiados para analizar datos.

• Explicar curvas Gaussianas/Normales
• Explicar Media/Desviación estándar
• Explicar cómo se calculan los P-valores
• Introducir errores Tipo I y Tipo II

• Actividad Distribución normal ajustada
• Actividad Folleto de datos de multi-funciones
• Actividad Distribución normal
• Actividad Distribución sesgada
• Taller  Gaussianas superpuestas. Preguntas de exploración 
• Taller  Gaussianas superpuestas. Preguntas de exploración(doc)