Inicio Discusiones Funciones y conceptos del álgebra El uso de residuos para identificar una recta de buen ajuste

Actividades Diccionario Herramientas Lecciones Discusiones Estándares

Discusiones

Temas
Funciones y conceptos del álgebra Álgebra de un paso Algoritmo Caos Coeficientes de correlación Cómo obtener información de los gráficos Coordenadas polares Criptografí­a y cifrados De gráficos a máquinas de funciones y viceversa Deducción de cónicas Desigualdades Diagramas de Venn Diagramas de Venn. Principiante El caos está en todas partes El uso de residuos para identificar una recta de buen ajuste Energía Exponentes y logaritmos Funciones de dos variables Funciones lineales Funciones múltiples Graficación del tiempo, distancia, velocidad y aceleración Graficar funciones en el sistema de coordenadas polares Gráficos imposibles Gráficos imposibles Introducción al plano coordenado y coordenadas Introducción al plano de coordenadas y a las coordenadas Inversos. Propiedades Las funciones como procesos o reglas Las funciones y la prueba de la recta vertical Pendiente e intercepto de Y Propiedad distributiva Propiedad distributiva Propiedades de identidad Recogiendo información a partir de gráficas Recta de mejor ajuste Recta de mejor ajuste Recurrencias Recursión Tiempo transcurrido Tiempo transcurrido Dos Uso de residuos para identificar una recta de buen ajuste Variables independientes y variables dependientes Cálculo Matemáticas discretas Geometría y medición Modelado Números y operaciones Probabilidad Estadística Trigonometría Otra

El uso de residuos para identificar una recta de buen ajuste

Explica cómo los residuos pueden determinar si una recta es un buen ajuste o un mal ajuste para un conjunto de datos bivariados

Mentor: Para ver si una recta es un buen o un mal ajuste para un conjunto de datos podemos examinar los residuos de esa recta.

Estudiante:  ¿Por qué los residuos tienen relación con la decisión de si una recta es un buen ajuste?

Mentor: Bueno, los residuos expresan la diferencia entre los datos sobre la recta y los datos reales así que los valores de tales residuos muestran qué tan bien representan los datos.

Estudiante: OK. Bueno, ¿en qué debo fijarme cuando examino los residuos? 

Mentor: Bien, si la recta es un buen ajuste para los datos, entonces la gráfica de residuos será aleatoria. Sin embargo, si la recta es un mal ajuste para los datos entonces el gráfico de residuos tendrá un patrón.

Estudiante:  ¿Cómo se verían los datos que forman un patrón comparados con datos aleatorios?

Mentor: Démosle un vistazo a un conjunto de datos con un buen ajuste y a un conjunto de datos con mal ajuste, para ver la diferencia. Primero, veamos los residuos de una recta que es un buen ajuste para un conjunto de datos. Utilizando la Actividad de Regresión grafica los datos  {(1, 3) (2, 4) (3, 3) (4, 7) (5, 6) (6, 6) (7, 7) (8, 9)}. Ahora, selecciona Mostrar la recta de mejor ajuste y selecciona Mostrar residuos. Ahora puedes ver el gráfico de residuos de todos los residuos obtenidos restando los valores de las predicciones de la recta de mejor ajuste de los valores reales.

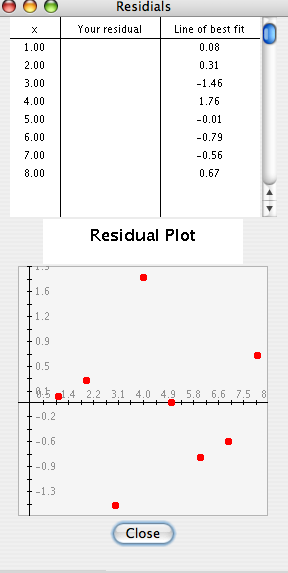
                                   Residuos
x                 Sus residuos          Recta de mejor ajuste


                            Gráfico de residuos 

                                   (Cerrar)

Estudiante: Los residuos aparecen aleatoriamente dispuestos en la gráfica. Puedo ver que se trata de un patrón aleatorio de residuos. ¿Cómo se vería un gráfico de residuos para una recta que es un mal ajuste para los datos? 

Mentor: Bueno, miremos otro gráfico. Utlizando la Actividad de Regresión grafica los siguientes puntos: {(4, -11), (3, -6), (2, -3), (1, -2), (0, -3), (-1, -6), (-2, -11)}. Corresponden a la gráfica de la ecuación cuadrática  -x^2 +2x-3. Ahora, selecciona Recta de mejor ajuste para graficar una recta que ajuste los datos. Selecciona enseguida  Mostrar residuos, para ver el gráfico de residuos que quieres examinar. 

 

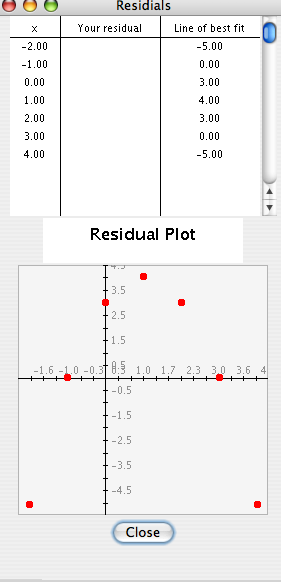
    Residuos
x                 Sus residuos          Recta de mejor ajuste


                            Gráfico de residuos 

                                   (Cerrar)

Estudiante:  ¡Hey, los residuos forman un patrón! Definitivamente no están esparcidos aleatoriamente, sino que forman una curva. Esta no era una recta de buen ajuste. ¿Habrá ocasiones en las que no se pueda decir si los residuos forman o no un patrón?

Mentor: Algunas veces no se tienen suficientes residuos que permitan ver un patrón definido en la gráfica, pero en la mayoría de los casos se puede ver el gráfico de residuos y, usando este criterio, determinar si la línea es un buen ajuste o un mal ajuste para los datos.

Estudiante:  Noté que los valores residuales (los valores que están en la columna de la derecha en la tabla anterior (bajo el texto Línea de mejor ajuste) parecen tener una suma cercana a 0. ¿Ayuda o no la suma de residuos a determinar si una recta es un buen ajuste para los datos?

Mentor: La suma de los residuos no necesariamente determina algo. La recta de mejor ajuste  con frecuencia tiene una suma cercana a 0 porque incluye todos los puntos de datos y por lo tanto estará  por encima de algunos puntos de datos y por debajo de algunos otros.  En consecuencia, en el caso de la recta de mejor ajuste el error positivo balanceará el error negativo de tal manera que la suma de los residuos será aproximadamente 0. No obstante, esto no significa que la recta sea un buen ajuste para los datos; solamente significa que la recta está igualmente por encima que por debajo de los datos reales. 

Estudiante: OK, ahora sé que para decidir si una recta es un buen ajuste para un conjunto de datos, puedo examinar el gráfico de residuos y si los residuos forman un patrón, entonces la recta no es un buen ajuste.