Inicio Actividades Números y operaciones Relojes en bases numéricas
Relojes en bases numéricas
Temas
Relojes en bases numéricas
¿En qué consiste la actividad Relojes en bases numéricas ?
Esta actividad le permite convertir, a base 10, números en una base diferente. El sistema numériico en que acostumbramos trabajar se llama de base 10 porque hay 10 dígitos, 0 hasta 9, En un sistema numérico de base 7 hay 7 dígitos: de 0 hasta 6.
En un sistema de números de base 12 habrá doce dígitos individuales que representan los valores 0 hasta 11. Cuando los sistemas de números tienen una base mayor a diez usamos, como dígitos, letras del alfabeto; por esto 10 y 11 se representarían con A y B respectivamente.
Los antiguos Mayas usaron la base 20 para su sistema de conteo y los Sumerios utilizaron la base 60. Los científicos de la computación utilizan con frecuencia la base 2 y también la base 16. La mayoría de la gente utiliza hoy la base 10. Hacer cálculos con horas y minutos o pies y pulgadas es semejante a calcular en base 60 o en base 12, respectivamente.
Recursos para la clase
- Actividad Aritmética del reloj
- Discusión sobre Base diez
- Discusión sobre Relojes y aritmética modular
- Discusión sobre Convertir desde base diez
- Discusión sobre Valor posicional
- Taller Preguntas de exploración sobre Relojes en diferentes bases
- Taller Preguntas de exploración sobre Relojes en diferentes bases (doc).
Actividad
¿Cómo puedo utilizar esta actividad?
Descripción
Esta actividad puede usarse para comprender otras bases para números. El usuario puede digitar un número y calcular ese número en una base diferente. La respuesta se despliega en tres relojes, uno para cada dígito y bajo ellos en forma numérica.
Controles y Resultados
La barra deslizante situada en la parte superior izquierda de la actividad le permite ajustar el valor de la base. La base por defecto es 10, la base mínima es 2 y la máxima es 16.
En el lado opuesto a la barra deslizante hay una caja de texto en la que usted puede entrar el número en base diez que quiere calcular en otra base. El número debe ser mayor o igual a cero y su valor máximo cambia dependiendo del valor de la base. El valor maximo (en base 10) es la base menos uno multiplicada por el cuadrado de la base.
Cuando haya ingresado el número, haga click en uno de los dos botones que hay junto a él, que dicen "paso a paso " o "cuenta". Si lo hace en "cuenta" el botón cambia a botón "parar" y usted puede usarlo para detener el cálculo y la animación.
"Cuenta" dará inicio al cálculo y animación de los relojes. Use el menú desplegable de animación para seleccionar qué tan rápida será la animación del reloj. Elija entre rápido, medio y lento, o escoja "No animar" si quiere ver el resultado pero no quiere mirar la animación.
"Paso a paso" también da inicio al cálculo, pero le permite ver la animación paso a paso.
Debajo de los relojes hay dos ecuaciones. La ecuación de la izquierda muestra cómo se expresa, en la base especificada, el número que usted ingresó. La ecuación de la derecha muestra cómo se expresa ese número en base 10.
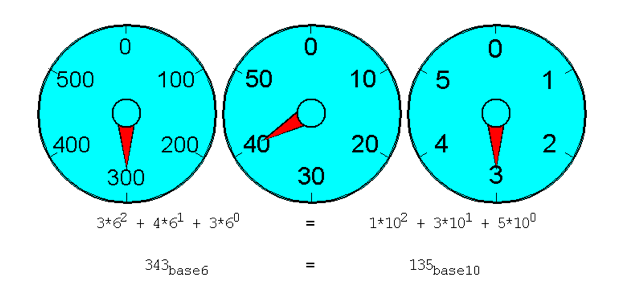
Cada reloj corresponde a un término en la ecuación de la izquierda. Los valores que muestra el reloj indican los posibles valores con los que cada término puede contribuir a la respuesta que usted ve frente a la base (en este caso 343). Así, el término de más a la derecha en este ejemplo puede contribuir con 0, 1, 2, 3, 4 o 5. (aquí contriibuye con 3) a la respuesta final.
Usted puede ver los valores en el reloj en la base escogida en lugar de en base 10, no chequeando la caja que hay junto a ''Relojes numéricos en base 10".
Si quiere ingresar otro valor después de haber ingresado alguno, haga click en "Reiniciar".
Recursos y contexto curricular
Esta actividad permite al usuario experimentar con la conversion de base 10 a otra base hasta base 16. La actividad es apropiada para trabajo en grupos durante unos 45 minutos, si utiliza las preguntas de exploración; si no lo hace, la actividad dura unos 15 minutos.
Ubicación en el currículo de matemáticas
- Comprender la aritmética modular
- Iniciar en la idea de sistemas de base diferente a la base 10
- Aprender a convertir de base 10 a otras bases
- Practicar la división larga (división entera) y trabajar con residuos de la división.
Estándares alcanzados
Grados 3-5
- Números y operaciones
- Calcular con agilidad y hacer estimaciones razonables
Grados 6-8
- Números y operaciones
- Entender los significados de las operaciones y las relaciones entre ellas
Grados 9-12
- Números y operaciones
- Comprender los números, las formas de representarlos, las relaciones entre los números, y los sistemas numéricos.
Esté preparado para:
- Explique qué es una "base"
- Muestre cómo convertir, a mano, un número dado en base 10 a otra base.
- Explique la diferencia entre numerar los relojes en base 10 y no numerarlos en base 10
- Responda la pregunta:"¿Por qué algunos relojes tienen letras?
- Responda la pregunta: "¿Por qué algunas bases tienen cuatro relojes y algunos solamente tres?
Recursos para clases
- Actividad Aritmética del reloj
- Discusión sobre Base diez
- Discusión sobre Relojes y aritmética modular
- Discusión sobre Convertir desde base diez
- Discusión sobre Valor posicional
- Lección sobre Aritmética modular
- Lección sobre Relojes para números base
- Taller Preguntas de exploración sobre Relojes en diferentes bases
- Taller Preguntas de exploración sobre Relojes en diferentes bases (doc).
