Estudiante: ¿Cuál es la propiedad distributiva?

Mentor: Bueno, la propiedad distributiva establece que el producto por la suma o la diferencia de dos números es el mismo que la suma o diferencia de sus productos. Por ejemplo, 2*(5-3) tiene el mismo valor de 2*5 - 2*3. La propiedad distributiva se utiliza si hay un número (o variable) que debe multiplicarse por una adición o sustracción incluida en paréntesis. 

Estudiante: No veo cómo  2*(5-3) y  2*5 - 2*3 pueden tener el mismo valor

Mentor: Usemos primero la propiedad distributiva para resolver este problema, hallando la diferencia de los productos. ¿Esto significa hacer que?  

Estudiante:  El 2 que está afuera del paréntesis debe multiplicarse por los números 5 y 3 del paréntesis? 

Mentor: Sí; de acuerdo con la propiedad distributiva debemos multiplicar el 2 pr cada uno de los números y conservar el signo que está entre esos números. Entonces, debes primero multiplicar  2 por 5. ¿Cuál será la respuesta?

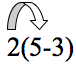
Estudiante: 2*5=10.

Mentor: Y ahora debes mantener el signo menos y escribirlo después del 10, de tal manera que hasta ahora esto se ve como  10 - __. A continuación debes multiplicar el 2 por el 3. ¿Cuál es la respuesta? 

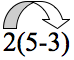
Estudiante: 2*3 = 6.

Mentor: Correcto, entonces tu respuesta para  2*5 - 2*3 sería: 10 - 6. Ahora haces esta sencilla resta y ¿qué obtienes?

Estudiante: 10-6 = 4. Entonces la respuesta es 4.

Mentor: Veamos si la respuesta es la misma cuando calculamos la resta del paréntesis y  la multiplicamos por el número de afuera del paréntesis, de tal manera que estamos encontrando el producto por la diferencia. 

2(5-3) => 2(2) = 4.

Estudiante: ¡Da lo mismo! De cualquier forma que resolvamos el problema, si encontramos el producto de la diferenca de dos números en paréntesis o la diferencia de sus productos, obtenemos el mismo resultado.  

Mentor: Exacto. Tratemos ahora usando una variable y aplicando la propiedad distributiva. Resolvamos este problema: 

-4 + x(3 - x) = ?

Estudiante: Primero usaría la propiedad distributiva, así que multiplico  "x" por  3. Me da 3x.

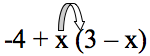
A continuación escribo el signo menos después de "x" y después multiplico la  "x" por la  "x" del paréntesis y esto me da x^2.

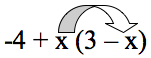
Mentor: ¡Muy bien! Entonces, ¿cuál seria la diferencia de sus productos?

Estudiante: 3x - x^2. Pero debo asegurarme de incluir el -4 inicial, y por lo tanto la solución final sería:  -4+3x-x^2.

Mentor: ¡Bien! Tratemos ahora de despejar "x" usando la propiedad distributiva.

Despejar "x" en esta igualdad: 4= -5(x + (-2))

Estudiante: Primero aplicaría la propiedad distributiva empezando al comienzo del paréntesis y multiplicaría (-5) por "x"  para obtener (-5x).

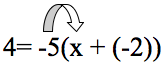
A continuación escribiría el signo de la suma que está en el paréntesis entre los dos valores. Después multiplicaré el (-5) por (-2) que es 10. 

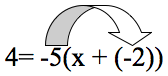
Mentor: Entonces, ¿qué tienes hasta aquí?

Estudiante: 4 = (-5x) + 10

Mentor: Ahora puedes despejar "x".

Estudiante: Correcto.  Entonces quiero tener  solamente "x" en uno de los lados. Para hacerlo restaré 10 en ambos lados, así: 

4 - 10 = (-5x) + 10 - 10 => 4-10 = (-5x)

Ahora calculo 4-10 que es -6, con lo cual mi problema se reduce a:

-6 = (-5x)

En este  momento debo dividir ambos lados por (-5) para dejar sólo a "x" en un lado. Entonces, la solución es:

6/5 = x

Mentor: ¡Buen trabajo! Usaste la propiedad distributiva para despejar  "x". Revisemos lo que hiciste. El problema original era 4= -5(x + (-2)) así que reemplazaré "x" con (6/5) pues encontraste que este es el valore representado por "x"
 

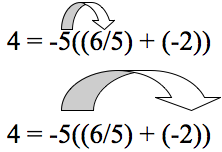
Aquí usaré la propiedad distributiva y haré las operaciones, obteniendo: 4 = -6 + (10). Finalmente, una simple adición: 4 = 4. ¡Felicitaciones; encontraste el valor correcto para  "x"!