Mentor: En nuestra última discusión hablamos sobre conjuntos. ¿Me explicas qué es un conjunto? 
Estudiante 1: Si, un conjunto es un grupo de objetos que tienen aspectos similares como el color, el tamaño o la forma. Cada objeto individual se llama un elemento. 

Mentor: Si tengo conjuntos de dos figuras, ¿es posible que los conjuntos tengan elementos comunes? ¿Puede un elemento estar en ambos conjuntos? 

Estudiante 2: Si, porque los conjuntos pueden clasificarse por diferentes aspectos. Un elemento puede estar en un conjunto a causa de su color y en otro en virtud de su tamaño. 

Mentor: ¡Muy bien! Entonces hay elementos que pueden hacer parte de dos conjuntos a la vez. Voy a hacer un diagrama que represente esto y tú puedes ayudarme colocando algún elemento en la parte correcta.

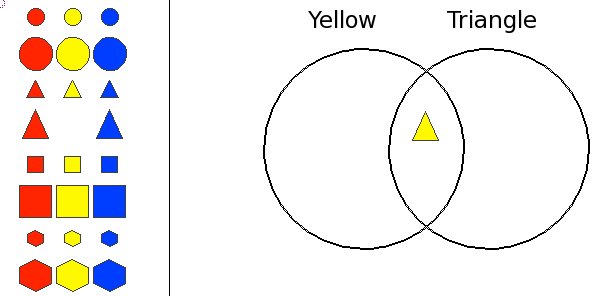
                                                                               Amarillo                             Tiángulo

Mentor: Yo puse el triángulo en la región en que los dos círculos se traslapan. ¿Por qué crees que lo hice así?

Estudiante 1: Bueno, es un triángulo, pero es también amarillo, así que hace parte de los dos conjuntos y debería ir en ambos círculos. Dada la forma en la que usted los dibujó, es claro que la región de traslape representa pertenencia a ambos círculos. 

Mentor: Entonces, ¿cómo deberíamos llamar a estos círculos? 

Estudiante 2: Cada círculo es un conjunto. 

Mentor: ¡Correcto! ¿Puede alguno pensar en otra figura que yo pudiera poner en este diagrama? ¿Qué tal una figura que es amarilla pero que no es un triángulo?

Estudiante 1: Puede poner el pequeño círculo amarillo en el círculo "amarillo",  pero no en el círculo "triángulo" porque no es una figura de tres lados. 

Mentor: ¡Exactamente! Lo que estamos haciendo se llama un Diagrama de Venn. Algunas veces usamos diagramas de Venn con dos círculos, como el que acabamos de dibujar, y algunas veces es mejor usar uno con más de dos círculos. Tratemos de crear un diagrama de Venn con tres círculos. 

Estudiante 2: Para crear un diagrama de Venn con tres círculos se necesitan tres categorías o descripciones que puedan juntarse para crear conjuntos. 

Mentor: Lo importante  a tener en cuenta es que las categorias tienen que tener una intersección. ¿Qué creen que significa esto? 

Mentor: Algo así como que es posible que se tengan todas las categorías a la vez. Por ejemplo, las categorías verde, pequeño y de rayas pueden describir conjuntamente el mismo objeto. Pero, ¿y si dije que tenia un objeto grande, pequeño y azul? 

Estudiante 2: No le hubiera creído. No se puede ser grande y pequeño a la vez.

Mentor: ¡Exactamente! ¿Pueden darme ejemplos de tres categorías con las cuales construir un diagrama de Venn de tres círculos?

Estudiante 1: Para un diagrama de Venn de tres círculos podríamos usar las categorías círculo, rojo y grande.

Mentor: ¡Correcto! ¿Cuál sería una figura que iría en la región donde se traslapan los tres círculos?

Estudiante 2: El círculo rojo grande encaja en los tres. Pero el círculo grande y azul y el círculo grande y amarillo encajarian solamente en la intersección de grande con círculo. 

Estudiante 1: El pequeño círculo rojo iria en la intersección de rojo y círculo, mientras que el círculo amarillo pequeño y el círculo azul pequeño irían solamente en el conjunto de los círculos. El triángulo, el cuadrado y el exágono rojos grandes irían en la región de las figuras grandes y rojas. Las otras figuras ojas irían en el conjunto rojo, y las otras figuras grandes irian en el conjunto grande.

The small red circle would go in the intersection for red and circle, while the small yellow and small blue circle would only go in the circle set. The big red triangle, square, and hexagon would go in the area for big red shapes. The other red shapes would go in the red set, and the other big shapes would go in the big set.

Mentor: Los dos tienen razón. ¡Buen trabajo!