Inicio Discusiones Matemáticas discretas Recursión
Discusiones
Temas
Recursión
Estudiante: Hábleme de recursión. ¿Es lo mismo que iteración, o no?
Mentor: La recursión es un caso especial de iteración. Esta es la idea: En una recursión se nos da una información para empezar y una regla sobre cómo usarla para obtener nueva información. Entonces repetimos la regla usando la nueva información como si fuera la información de partida.
Estudiante: Entonces, ¿tenemos un bucle? Lo que resulta de aplicar la regla ¿regresa a la regla para la nueva iteración?
Mentor: Es una buena manera de describirlo. El siguiente es un ejemplo clásico de recursión; genera una sucesión de números llamada Números de Fibonacci. 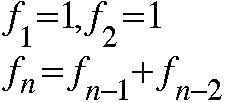
Aquí tenemos información de partida y una regla para generar un nuevo valor. La n se incrementa en 1 cada vez, por lo que podemos hacer preguntas como hallar el n-simo número de fibonacci. Se nos dan dos valores para empezar, puesto que cada nuevo valor se calcula a partir de los dos valores inmediatamente anteriores. Intenta generar el noveno número de fibonacci.
Estudiante: Veamos. Los primeros números son 1 y 1, valores dados. La regla indica tomar los dos números inmediatamente anteriores y sumarlos para obtener el nuevo número, así que tendríamos:
| n = 3: | 1 + 1 | = | 2 |
| n = 4: | 1 + 2 | = | 3 |
| n = 5: | 2 + 3 | = | 5 |
| n = 6: | 3 + 5 | = | 8 |
| n = 7: | 5 + 8 | = | 13 |
| n = 8: | 8 + 13 | = | 21 |
| n = 9: | 13 + 21 | = | 34 |
Mentor: ¡Bien! Consideremos ahora los ejemplos sobre fractales que hemos visto hasta aquí. Para fractales, la información de partida se llama el iniciador, la regla para iterar se llama el generador.
| Fractal | Iniciador | Generador | Después de varias iteraciones |
| Curva de Hilbert | Segmento de recta | 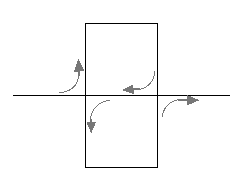 |
|
| Otra curva de Hilbert | Segmento de recta |  |
|
| Copo de nieve de Kock | Triángulo | 
Cada lado del triángulo |
|
Estudiante: Así que en cada uno de estos casos tenemos el estado inicial y la regla para moverse al estado siguiente
Mentor: ¡Sí!