Estudiante: ¿Qué es un residual?

Mentor: Un residual es la diferencia entre el valor medido y el valor de la predicción en un modelo de regresión lineal. Es importante entender los residuales porque muestran qué tan precisa es una función matemática, tal como una recta, que representa un conjunto de datos. Para encontrar un residual se resta el valor de la predicción del valor medido.

Estudiante: ¿Cuáles son los valores de la predicción? ¿Cómo los encuentra?

Mentor: La recta de mejor ajuste proporciona los valores de predicción para un conjunto de datos. Por ejemplo, con la recta de mejor ajuste el valor de predicción o pronóstico es el valor que corresponde en la recta a un valor específico de la variable independiente. Da una mirada a  la gráfica. Los valores de la coordenada x en la recta de mejor ajuste coinciden con los valores x del conjunto de datos.

Ahora usemos la actividad Regresión para calcular un residual. Primero, grafiquemos los siguientes cuatro datos: {(1, 2) (2, 4) (3, 6) (4, 5)}. Las etiquetas x y y se han utilizado para representar en la gráfica las variables independiente y dependiente respectivamente. Estos valores dados de y (variables dependientes) son los valores medidos para los valores especificados de x (variables independientes). Ahora grafiquemos la recta de mejor ajuste seleccionando Mostrar la recta de mejor ajuste y veamos dónde quedan en el gráfico los valores predichos por el modelo.

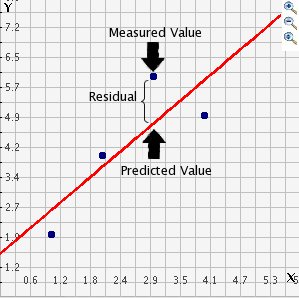
Estudiante: ¡Qué bien! Ahora entiendo qué quiere usted decir cuando habla de valores predichos por el modelo y valores observados.  

Mentor: Excelente. Ahora tratemos de hallar el residual para la variable independiente, x=1. ¿Cómo lo harías? 

Estudiante: Bueno, primero escribiría el valor medido para la variable independiente x=1, dado que grafiqué el punto (1, 2). Ahora observo que cuando el valor de x es 1, el valor de y sobre la recta de mejor ajuste es aproximadamente 2.6. Entonces, para hallar el residuo restaría el valor predicho del valor medido, así que el residual sería 2 - 2.6 = -0.6.

Mentor: ¡Muy bien! El residuo de la variable independiente x=1 es -0.6. Si tienes problemas para recordar qué valor restar de cuál, puedes pensarlo así: estás tratando de saber qué tan lejos del valor real está el valor predicho así que tomas el valor real y le restas el valor predicho por el modelo. A veces el residual es positivo y algunas veces es negativo. Cuando estés practicando la determinación de residuales puedes usar la actividad Regresión y seleccionar mostrar residuales, para comparar tus resultados. 

Estudiante: ¡Qué bueno! El valor 1 bajo la columna X se corresponde con el número -0.6 bajo la columna recta de mejor ajuste. El residual para x=1 es -0.6. Entonces, ¿los números en la columna recta de mejor ajuste son los residuales para el correspondiente valor de x?

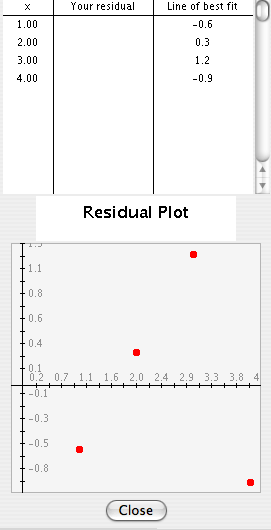x       Su residual      Recta de mejor ajuste

                                                                                                                    Gráfico de residuales
                                                                                                                              Cerrar 

Mentor: Sí. Además, en la gráfica de residuales los valores de y son los residuales correspondientes a los valores de x. Esta gráfica es una forma visual de representar los residuales de variables independientes y dependientes. 

Estudiante: Esto es realmente útil. ¡Ya sé cómo calcular residuales!