Estudiante: ¿Qué es un valor atípico?

Mentor:  Un valor atípico se define como un valor que está lejos de la mayoría de los otros en un conjunto de datos. Por ejemplo, dados estos puntos: {(1,0) (2,2) (3,3) (4,5) (5,5) (7,6) (7,7) (8,1)}, ¿cuál crees que es el dato atípico? Puede ser más claro si los graficamos: 

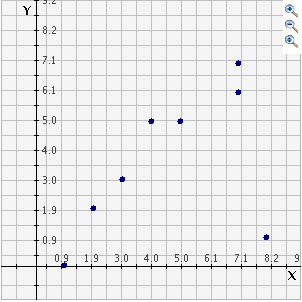
Estudiante: Bueno, todos esos puntos forman casi una recta diagonal, con excepción de (8, 1) que parece estar lejos de la mayor parte de los otros puntos, tal como lo dice la definición de datos atípicos.

Mentor: ¡Buen trabajo! Un dato atípico puede causar problemas cuando tratas de sacar conclusiones a partir de tus datos.

Estudiante: ¿Qué clase de conclusiones?

Mentor: Con gráficas como esta que usan coordenadas, a menudo tratamos de ver si hay una relación entre los valores de x y de y que pueda establecerse con la recta de mejor ajuste. Entonces, si graficáramos la recta de mejor ajuste para estos puntos obtendríamos esto: 

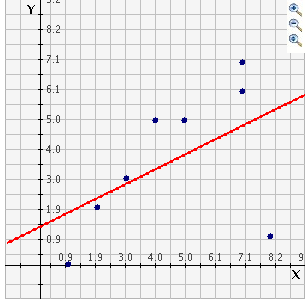
Estudiante: Yo hubiera pensado que la recta pasaría por más puntos. 

Mentor: Exactamente. Pero se ve así por causa del dato atípico. Este dato hace que la pendiente de la recta de mejor ajuste sea menor de lo que se podría esperar. Si descartamos el dato atípico, (8, 1), la gráfica se vería así: 

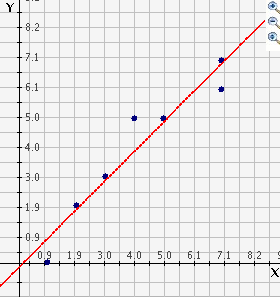
Estudiante: Me doy cuenta de que el dato atípico estaba afectando la recta. 

Mentor: Otra conclusión que puede extraerse de los datos es la media, que también se ve afectada por los valores atípicos. Veamos un ejemplo: Consideremos las estaturas de un grupo que incluye a cinco estudiantes de segundo grado y también a su profesor. Sus alturas, en pulgadas, son 48" 46" 48" 50" 44" y 72".

Estudiante: La estatura del profesor es un valor atípico. No está para nada cerca de las otras medidas. 

Mentor: Bien. ¿Puedes hacer una gráfica en una recta numérica? 

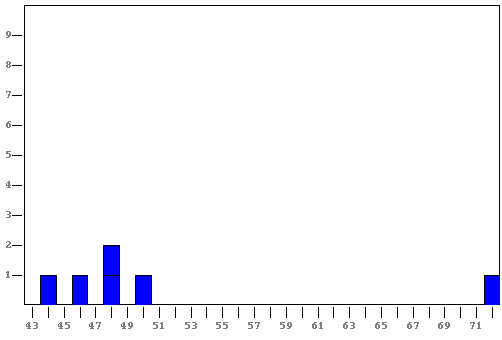
Mentor: Bien. Ya puedes ver que el dato atípico está muy lejos del resto de datos. Como te dije anteriormente, los datos atípicos pueden afectar la media. ¿Cuál es la  media de estos datos?

Estudiante: Pues, para hallar la media, sumo todas las estaturas (lo cual da 308) y divido por el número de personas (en este caso 6) y, por lo tanto, la media es 51"

Mentor: ¿Consideras que 51" es una representación adecuada de las estaturas?

Estudiante: No, el estudiante más alto mide solamente 50"; por lo tanto, 51" no representa adecuadamente las estaturas de los estudiantes. 

Mentor: De acuerdo. El 72" está influyendo en la media. Calculemos ahora la media, sin incluir la altura del profesor. 

Estudiante: Muy bien, sumo todas las alturas, lo cual da 236, y divido entre el número de personas, en este caso 5. Entonces la media es más o menos 47", valor más representativo de las estaturas del grupo de estudiantes.   

Mentor: Sí, 47" es una mejor representación de los datos. Entonces, ahora sabes que si hay un dato atípico entre tus datos, probablemente necesitas examinarlos más detenidamente para decidir si lo conservas o no para el análisis de los datos.