Inicio Discusiones Geometría y medición Algoritmo Perímetro
Discusiones
Temas
Algoritmo Perímetro
Estudiante: ¿Hay alguna forma de calcular el perímetro de estas formas aleatorias sin tener que contarlo todo?
Mentor: Sí la hay. Veamos este ejemplo. El primer paso es "encajonar" el objeto. Después se calculan la longitud y el ancho de "la caja".
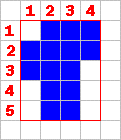
Estudiante: En este ejemplo la longitud es 4 y el ancho es 5.
Mentor: Ahora, calculemos el perímetro de "la caja". El perímetro es la distancia alrededor de "la caja", que es:
Largo + Ancho + Largo + Ancho = 2 Largo + 2 Ancho
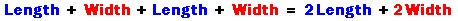
Estudiante: En este ejemplo el perímetro es dos por cuatro más dos por cinco.
Mentor: Sí. Y recuerden que debemos multiplicar primero y sumar después, que es el orden de las operaciones. Por lo tanto el perímetro de "la caja" es ocho más diez, es decir, dieciocho.
Estudiante: Ahora sabemos cuál es el perímetro de "la caja", pero ¿esto qué tiene que ver con el perímetro del objeto?
Mentor: ¡Son iguales!
Estudiante: No es posible que sean iguales, eso no tiene sentido.
Mentor: Tiene sentido, si observas en el dibujo siguiente el número de lineas perimetrales por fila y por columna. Los números en azul son las líneas perimetrales del objeto en esa columna o fila y los números en rojo son las líneas perimetrales de "la caja".
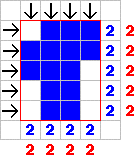
Ahora puedes ver que el perímetro de "la caja" es realmente igual al perímetro del objeto.
Estudiante: Chévere, ¿y el truco funciona con todas las figuras?
Mentor: No, no funciona con figuras que se doblan sobre sí mismas. Sumando un bloque a nuestro ejemplo se ve que el truco no funciona. ¿Alguien sabe por qué?
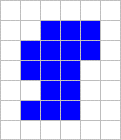
Estudiante: Antes usted nos dijo que deberiamos ver el dibujo como el número de lineas perimetrales por fila y por columna. En esta imagen el número de lineas perimetrales de la figura no coincide con el número de líneas perimetrales de "la caja".
Mentor: ¡Buen trabajo! En la primera columna hay cuatro líneas perimetrales de la figura pero la caja tiene solamente dos. En consecuencia el perímetro del objeto es dos más que el perimetro de "la caja". El perímetro de la figura es dieciocho más dos, es decir, veinte.
Estudiante: Entonces, cuando la figura se dobla sobre sí misma, tenemos que observar detenidamente las columnas y las filas para determinar cuántas lineas perimetrales tiene de más y sumarlas al perímetro de la caja.
Mentor: ¡Buen trabajo! Juguemos ahora con la aplicación Explorador de perímetro y veamos qué tan bien funciona nuestro método.
