Estudiante 1: ¿Cómo podemos saber qué tanto puede contener en su interior (su volumen) un objeto tridimensional?

Mentor: Bueno, hay diferentes maneras de hallar el volumen, que dependen de la forma del objeto tridimensional. Veamos primero una forma de caja. ¿Cómo consideras que se puede encontrar el volumen de esta figura?

Estudiante1: Bueno, hallamos el área de un rectángulo multiplicando el largo por el ancho esto nos muestra qué tanto de un rectángulo plano se ha llenado, entonces ¿será que hacemos algo similar para hallar el volumen de una figura rectangular tridimensional?

Mentor:¡Bien pensado! Estás muy cerca. Una figura plana se llama bidimensional porque tiene dos dimensiones (en el caso de un rectángulo se llaman el largo y el ancho) en tanto que una figura tridimensional tiene tres dimensiones. Veamos una forma rectangular tridimensional (un prisma rectangular)

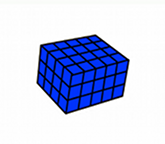
Mentor: Esta figura tiene un largo y un ancho, tal como mencionaste que tienen los rectángulos planos. Pero, ¿qué más tiene esta figura tridimensional que las figuras planas no tienen? ¿Cuál es la dimensión extra?

Estudiante 2: Hay otro lado que muestra qué tan profunda es.

Mentor: Correcto, se llama la profundidad. La profundidad es lo que hace que esta figura sea tridimensional puesto que tiene tres dimensiones: longitud, anchura y profundidad. Estas tres dimensiones se usan para hallar el volumen de un prisma rectangular. Para hallar el área de un rectángulo bidimensional multiplicamos el largo por el ancho, entonces empecemos hallando el área de una parte bidimensional de un prisma rectangular. Primero consideraremos  la capa superior del prisma rectangular en la que hay largo y ancho pero no hay profundidad.

Mentor: ¿Cuál es la longitud (llamada algunas veces la altura) de esta figura? 

Estudiante 1: 3.  Hay tres cubos a lo largo de los lados que van de arriba hasta abajo

Mentor: Muy bien, entonces la longitud es 3. Ahora, ¿cuál es el ancho?

Estudiante 2: El ancho es 5. Hay cinco cubos a lo largo de los lados que van de izquierda a derecha.

Mentor: ¡Es correcto! Ahora podemos calcular el área de esta figura plana. ¿Cómo lo hacemos?

Estudiante 2: Multiplicando el largo (3) por el ancho (5). La respuesta es 15.

Estudiante 1: ¡Tenemos que incluir la profundidad!

Mentor: Correcto. Miremos otra vez nuestra figura tridimensional

Mentor: Observa que la figura rectangular plana que vimos es solamente una capa de esta figura grande. Piénsalo así: La figura rectangular plana que vimos está apilada sobre otras figuras idénticas a ella.¿Cuántas figuras planas están apiladas en esta figura tridimensional?

Estudiante 1:¿Dijimos que la tercera dimensión, la profundidad, es 4? 

Mentor: Ahora, sabiendo que en la figura tridimensional hay cuatro capas de la figura plana que vemos, y sabiendo que la figura plana tiene un área de 15 bloques ¿cómo consideras que encontraremos el volumen?

Estudiante 2: Si hay cuatro capas, cada una con un área de 15, podemos sumar 5+15+15+15 y eso nos dará el volumen total. 

Estudiante 1: También pudimos multiplicar el área de la figura plana, 15, por 4. Es lo mismo que sumar el área de 15 cuatro veces.

Mentor: ¡Muy bien! ¿Y qué obtienes cuando multiplicas 15 por 4? 

Estudiante1: 60. ¡El volumen del prisma rectangular es 60!

Mentor: ¡Excelente trabajo! Hallaste el volumen de un prisma rectangular. Estos son los paso que dimos para hallar la respuesta.:

• Largo x ancho = Área de la figura rectangular plana.
• Área x profundidad = Volumen del prisma rectangular

Mentor: Por lo tanto, para calcular el volumen de un prisma rectangular multiplicamos largo, por ancho por profundidad.