Mentor: ¿Alguien puede decirme qué significa área de una superficie?

Estudiante 1: Es el número de unidades cuadradas que se necesitan para cubrir la superficie de una figura tridimensional.

Estudiante 2:  El área de la superficie es precisamente lo que se ve de un objeto tridimensional, no lo que está por dentro.

Mentor: Bien, ¿cómo calculan el área de la superficie de un objeto tridimensional?

Estudiante 1:  Bueno, hay muchos objetos tridimensionales como conos, prismas rectangulares y prismas triangulares. La fórmula para hallar el área de la superficie no puede ser la misma para todas estas figuras. 

Mentor: ¡Eso es verdad! Las fórmulas para el área de la superficie de las figuras tridimensionalews son diferentes y dependen de su forma. Examinemos específicamente la del prisma triangular.

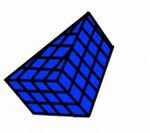
Mentor: Como vamos a calcular el área de la superficie de esta figura, ¿cuántas caras tenemos que incluir? 

Estudiante 1:  Este es un prisma triangular, así que tiene 5 caras (las dos caras triangulares y tres caras rectangulares). Tenemos que estar seguros de contar cuántas unidades cuadradas hay en cada una de ellas. Esto nos dará el área total que envuelve a la figura. 

Mentor: ¡Muy bien! Veamos primero la cara superior de esta figura. ¿Cuántas unidades cuadradas cubren esta superficie triangular?

Estudiante 2: Usted me pide encontrar el área. Recuerdo que el área de un triángulo es 1/2 del área de la base, multiplicada por la altura.

Mentor: Para esta actividad, a la base del prisma triangular la llamaremos ancho de la base y a la altura del prisma, profundidad de la base. 

Estudiante 1: OK, entonces el ancho de la base es 4 unidades y la profundidad de la base es 6 unidades. Por lo tanto, el área sería:

1/2 x 4 x 6 = 12 unidades cuadradas.

Mentor: Correcto. Ahora, ¿hay otra superficie idéntica a esta en el prisma triangular? 

Estudiante 1: La superficie directamente debajo de esta (la otra cara triangular del prisma) debe tener la misma cantidad de unidades cuadradas.

Mentor: Es verdad, pero ¿por qué?

Estudiante 2: Bueno, la anchura de la figura triangular plana será la misma (4 unidades) y la profundidad de la base será la misma (6 unidades), por lo tanto el área también debería ser la misma. 

Mentor: Bien.  Hasta ahora tenemos dos de las superficies cubiertas (cada una 12 unidades cuadradas). Movámonos ahora hacia la cara que mira a la derecha. ¿Cuántas unidades cuadradas hay en esta superficie? 

Estudiante 1: Bueno, un lado parece que tiene exactamente 3 unidades, pero no estoy seguro de cuantas unidades tiene el otro lado. Se ve inclinado y no estoy seguro.

Mentor: Buena observación. El lado de 3 unidades corresponde a la altura del prisma. La otra longitud, la que te confunde se llama la altura inclinada. Puede ser difícil hallar la altura inclinada en un prisma triangular. En este ejercicio seguiré adelante y para ello te doy su valor: 6.32 unidades.

Estudiante 2: OK, si la altura inclinada es 6.32 y la altura del prisma es 3 unidades, entonces el área de esta cara sería 6.32 multiplicado por 3, lo que es igual a 18.96 unidades cuadradas.

Mentor: Correcto. Ahora, ¿hay otra superficie idéntica a esta en el prisma triangular? 

Estudiante 2: Sí, la superficie opuesta a esta sería idéntica puesto que también para ella la altura del prisma es 3 unidades y la altura inclinada es 6.32 unidades. 

Mentor: Excelente. Ya tenemos cubiertas cuatro superficies. Dos de ellas tienen 12 unidades cada una, y dos de ellas tienen 18.96 unidades cada una. Veamos la última cara que podemos observar en esta figura tridimensional. 

Estudiante 1: ¡Esta superficie es fácli! Hay 4 unidades en un lado y 3 unidades en el otro.

Mentor: Correcto. Las 4 unidades corresponden al ancho de la base y las 3 unidades a la altura del prisma. ¿Qué harías para hallar el área de esta figura?

Estudiante 1: Dado que es un rectángulo, todo lo que tengo que hacer es multiplicar los dos números. 4 (el ancho de la base) por 3 (la altura del prisma) lo cual me da el área del rectángulo: 12 unidades cuadradas. 

Estudiante 2: ¡S! Y esto significa que hemos encontrado el área de las cinco caras totales. Un prisma triangular tiene solamente cinco caras y por lo tanto ya tenemos todas las áreas que necesitamos. 

Mentor:  Correcto. Entonces tenemos: 

• dos superficies de 12 unidades cuadradas.
• dos superficies de 18.96 unidades cuadradas.
• una superficie de 12 unidades cuadradas.

Ahora,¿cuál es el área de la superficie total del prisma triangular?

Estudiante 1: Para encontrar el área de la superficie total necesitaría sumar todas las áreas que encontré. Sería:

• 12+12+
• 18.96+18.96+
• 12 = 73.92 square units!

Mentor: ¡Excelente trabajo! Acabas de encontrar el área de la superficie de un prisma triangular!