Inicio Discusiones Geometría y medición Explorador de perímetro
Discusiones
Temas
Explorador de perímetro
Estudiante: ¿Hay alguna manera de calcular perímetros sin tener que contar completamente?
Mentor: Sí, veamos un ejemplo. Lo primero es pensar en cómo hallamos el perímetro
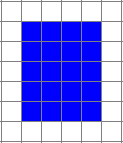
Estudiante: En este ejemplo el largo es 4 y el ancho es 5.
Mentor: Encontremos ahora el perímetro de la figura. El perímetro es la distancia alrededor de la figura, que es
largo + ancho + largo + ancho = 2 largo + 2 ancho
Estudiante: Para este ejemplo el perímetro es dos veces cuatro más dos veces cinco
Mentor: Así es. Ahora, recuerda que primero se multiplica y después se suma, de acuerdo conn el orden de las operaciones. Por lo tanto el perímetro de la figura es ocho más 10, que es igual a dieciocho.
Estudiante: ¿Podemos siempre multiplicar 2 por el largo, como en este caso?
Mentor: Es una buena pregunta. Tú me dirás. ¿Puedes pensar en un caso que no funcione así?
Estudiante: Si la figura es como esta:
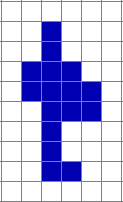
Mentor: Bien pensado. Pero en tanto estemos trabajando con rectángulos, siempre podemos usar nuestro algoritmo
largo + ancho + largo + ancho = 2 largo + 2 ancho
Estudiante: ¿Qué hacemos si es una figura simpática?
Mentor: Tienes un par de opciones. Siempre puedes usar este otro algoritmo. Pero, ¿qué crees que podrias hacer? Algoritmo para perímetro (Discusión)
Estudiante: PIenso que posiblemente hay que contar todo alrededor de la figura..
Mentor: Exactamente, y si son cuidadosos obtendrán siempre la respuesta correcta. Juguemos ahora con la actividad Explorador de perímetro y vemos qué tan bien funciona.
