Mentor: Si cortas una rebanada de un cubo, ¿qué forma tiene la figura que se crea?

Estudiante:  ¡Un cuadrado!

Mentor: ¿Siempre es así? ¿Y si el corte se hace en un ángulo?

Estudiante: Bueno, entonces dos de los lados serían más largos que los otros dos, por eso creo que la figura formada sería un rectángulo.

Mentor: Correcto. Ahora, ¿qué pasaría si el corte se hace en un ángulo diferente, digamos, si se corta una punta del cubo? 

Estudiante: Entonces...creo que se formaría un triángulo, algo así:

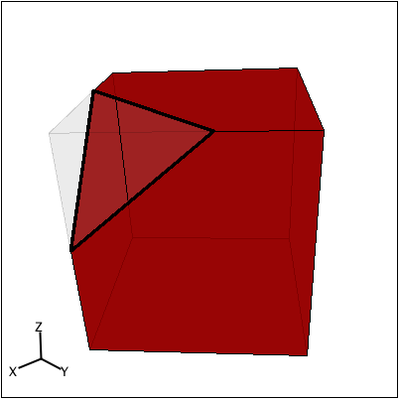
Mentor: ¡Exactamente! ¿Qué otras figuras piensas que se formarían cortando una sección transversal de un cuadrado?

Estudiante: Hmm, bueno, apuesto a que si se puede formar un triángulo cortando una esquina del cubo, entonces se puede crear un pentágono cortando un trozo más grande, así: 

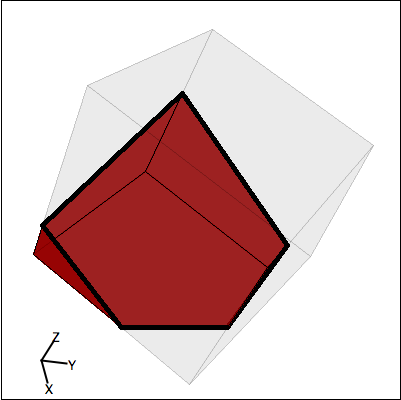
Mentor: Correcto; como ves, se puede crear una sección transversal con más lados que la figura original. ¿Qué pasaria si hicieras un ángulo tal en la sección transversal que una esquina superior de la sección transversal también fuera cortada? 

Estudiante: Entonces se tendría..¡un hexágono!

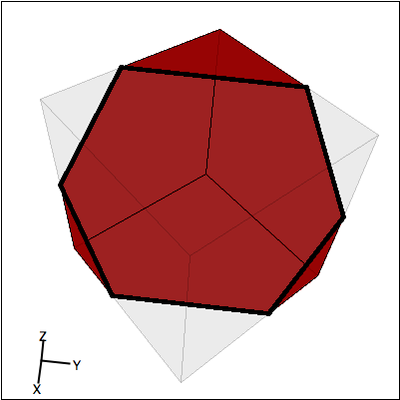
Mentor: ¡Exactamente! ¿Crees que puedas construir una figura con más lados, como un heptágono?

Estudiante: No me puedo imaginar como hacerlo dado que no puedo ver cómo cortar más de dos de las cuatro esquinas

Mentor: No te preocupes, lo que te pedí realmente es imposible. Hay solamente seis caras en un cubo y por lo tanto el máximo número posible de lados es seis. 

Estudiante:  Tiene sentido. Apostaría a que se puede hace lo mismo con cualquier prisma; -se trata simplemente de "angular" la sección transversal de tal manera que se intersecten todas las caras. 

Mentor: Tienes razón, cualquier prisma se puede cortar de tal manera que la sección transversal tenga tantos lados como el número de caras del prisma. Sin embargo, no todas las figuras tienen esta misma propiedad. ¿Podrías pensar en una figura de 3 dimensiones tal que no todos sus lados puedes ser cortados mediante el mismo plano?

Estudiante: Tal vez un icosahedro, porque no hay un plano que pueda intersectar sus veinte caras.

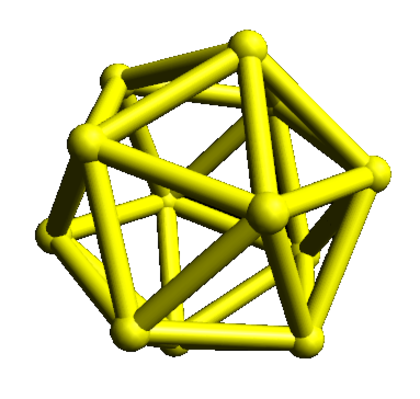
Mentor: Bien, el icosahedro es un ejemplo de un poliedro que no es un prisma. Si sólo consideramos prismas, ¿qué les pasaría a las secciones transversales de un prisma si el número de caras laterales tendiera a ser infinito?

Estudiante: Yo nunca he oído de un prisma con un número infinito de lados. .

Mentor: Bueno, cuando estés tratando de visualizar algo que no habías visto antes, trata de edificar sobre lo que ya conoces. Imagina un cuadrado, luego un pentágono regular, después un hexágono regular, etc. A medida que el número de lados se hace más grande, ¿a qué otra forma se aproxima la figura?

Estudiante: Hmm, empieza a parecerse más y más a un círculo, porque no se pueden ver los lados individuales.

Mentor: Exactamente. De hecho, los matemáticos definen formalmente el círculo como un polígono regular con un número infinito de lados. Entonces, ¿qué pasaría si se corta un prisma circular, conocido también como cilindro?

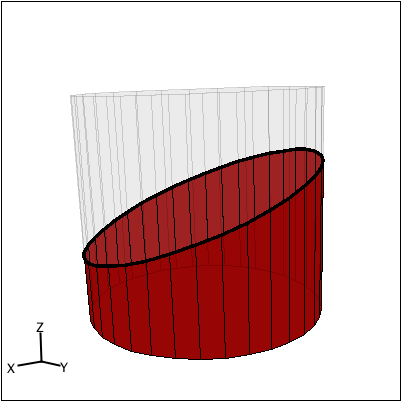
Estudiante: Bueno, obviamente se puede obtener un círculo si se hace un corte horizontal, y u

rectángulo si se corta verticalmente. Más interesante aún, sin embargo, es el hecho de que se puede obtener un óvalo si el corte con el cilindro forma un ángulo. 

Mentor: Hay un número infinito de figuras tridimensionales, cada una con su propia sección transversal. De hecho, cada figura bidimensional se puede definir como la sección transversal de una figura tridimensional. Esto es muy conveniente cuando se discuten las secciones cónicas, pero también será muy útil si decides estudiar Cálculo multivariado y otros cursos de matemáticas avanzadas. 

Estudiante: ¿Por qué definir figuras bidimensionales como secciones transversales? ¿Por qué no simplemente dejarlos en dos dimensiones? 

Mentor: Cuando se trabaja con figuras bidimensionales usualmente es más sencillo dejarlas en dos dimensiones. Pero un uso más intenso de las secciones transversales se da cuando se calcula el volumen de figuras irregulares. Cuando tomes el curso de Cálculo aprenderás cómo calcular el áres de casi todas las figuras bidimensionales. Y puesto que un objeto tridimensional se puede dividir en un gran número de secciones transversales, las áreas de tales secciones se pueden usar para calcular el volumen del objeto tridimensional.