Inicio Discusiones Geometría y medición Dimensión y escala
Discusiones
Temas
Dimensión y escala
Estudiante: Yo sé qué son dimensiones:
- Los puntos tienen dimensión 0
- Las rectas tienen dimensión 1
- Las figuras planas, como los cuadrados, tienen dimensión 2
- Los volúmenes sólidos, como los cubos, tienen dimensión 3
Mentor: ¡Bien! ¿Qué podemos aprender de tales afirmaciones? Empecemos con una recta puesto que los puntos no son de interés en lo relativo a fractales.
Las rectas tienen longitud pero no tienen anchura o altura, así que las podemos medir sólo en una dimensión. Debido a esto decimos:
La dimensión Euclidiana de la recta es 1.
Considera este segmento de recta:
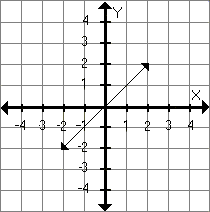
Construyamos ahora segmentos de recta semejantes, a menor escala. Utilizaremos un factor de escala de 4 (el segmento largo es 4 veces más largo que los cortos).
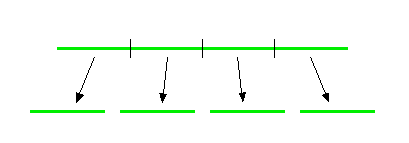
Observa que con este factor de escala podemos obtener 4 segmentos de recta "auto-similares" a partir del segmento original. Entonces: Dimensión=1, Escala = 4 y Número de objetos auto-similares=4.
Inténtalo con un cuadrado (figura plana)
Estudiante: Ok: La dimensión Euclidiana de un cuadrado es 2 porque podemos medir la longitud y la altura, pero no hay espesor. Consideremos este cuadrado:

Construyamos ahora cuadrados similares a menor escala. Usaremos un factor de escala de 3 (el lado del cuadrado grande es 3 veces más largo que el de los pequeños).
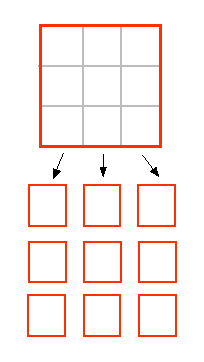
Observe que con este factor de escala podemos obtener 9 cuadrados "auto-similares" a partir del cuadrado original. Entonces: Dimensión=2, Escala = 3 y Número de objetos auto-similares=9.
Mentor: Hagamos juntos un cubo (sólido): La dimensión Euclidiana de un cubo es 3 porque podemos medir la longitud, el ancho y la altura. Consideremos el siguiente cubo:

Construyamos ahora cubos similares a menor escala. Usaremos un factor de escala de 2 (el lado del cubo grande es 2 veces más largo que el de los pequeños).
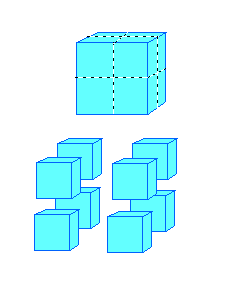
Observa que con este factor de escala podemos obtener 8 cubos "auto-similares" a partir del cubo original. Entonces: Dimensión=3, Escala = 2 y Número de objetos auto-similares=8.
Mentor: ¿Qué patrón ves aquí?
Estudiante: Dimensión, Escala y Número de copias parecen seguir este patrón:
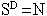
Mentor: ¡Bien! ¡Los fractales son objetos que tienen dimensiones fractal! Para ver esto necesitamos aprender cómo hallar D cuando conocemos S y N. Esto no es trivial dado que D está en el exponente. Necesitamos hablar de Exponentes y Logaritmos.
