Inicio Discusiones Geometría y medición Secciones cónicas
Discusiones
Temas
Secciones cónicas
Mentor: Hoy hablaremos de secciones cónicas. ¿Saben cuáles son las cuatro secciones cónicas?
Estudiante: Son la Parábola, Hipérbola, Elipse, and Círculo,¿no?
Mentor: Correcto. Si observan las gráficas de cada una de estas secciones cónicas, verán que son muy diferentes.
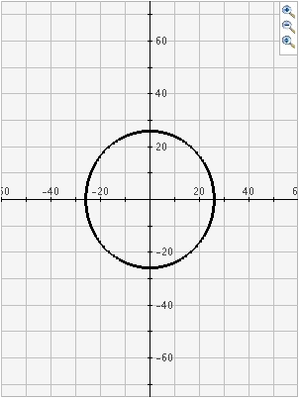
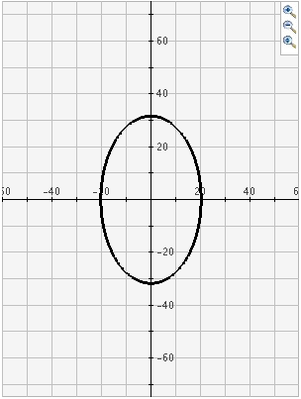
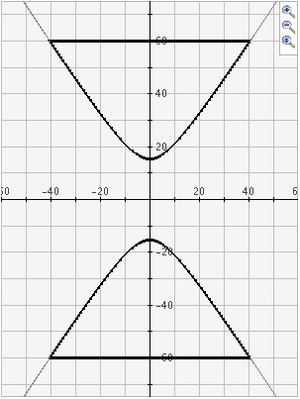
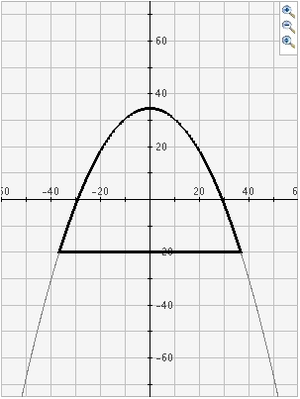
¿Qué supones es lo que las hace ser secciones cónicas?
Estudiante: ¿Tienen que ver algo con conos?
Mentor: ¡Absolutamente! Todas las gráficas se pueden formar con el mismo proceso. Primero que todo, ¿qué es una sección recta?
Estudiante: Es cuando se corta un objeto tridimensional con un plano, creando un objeto bidimensional.
Mentor: ¡Exactamente! Las secciones cónicas son precisamente secciones rectas de un cono doble . ¿Qué significa un "cono doble"?
Estudiante: Son dos conos, ¿cierto? donde los conos casi ni se tocan.
Mentor: Correcto. ¿Por qué necesitaría dos conos para formar secciones cónicas? ¿Cuál de estas secciones necesita dos conos?
Estudiante: La hipérbola tiene dos ramas y por eso se necesitan dos conos para crearla.
Mentor: ¡Muy bien! Según la forma en la que se corten los conos se formará cada una de las diferentes secciones cónicas. ¿Pueden decir cómo crear cada una?
Estudiante: El círculo se forma cortando el cono doble con un plano paralelo a su base, así:
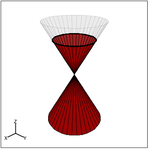
Y la parábola se forma cortando el cono doble paralelamente a su borde, de la siguiente manera:
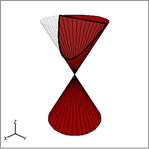
Exacto. Pensemos ahora en la elipse. Es una especie de mezcla entre parábola y círculo, verdad? Entonces, ¿de qué manera se corta el cono doble ?
Estudiante: La elipse es cualquier tajada entre una parábola y un círculo, ¿verdad? Como esto:
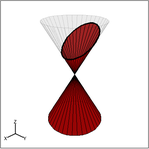
Mentor: ¡Exactamente! ¿Y con respecto a la hipérbola?
Estudiante: No sé, porque una parábola que intersecta a ambos conos es una hipéribola. ¿No sería lo mismo que una parábola?
Mentor: Pero dijiste que una parábola es algo paralelo al borde del cono. ¿Qué sabemos sobre la definición de paralelismo?
Estudiante: Cuando dos lineas son paralelas, nunca se intersectan. Entonces, si una parábola se crea por un corte que es paralelo al borde del cono, no puede ser una hipérbola. ¿Se crea una hipérbola cortando el doble cono en un punto cualquiera entre los planos de dos parábolas?
Mentor: That's right! Just like in this picture:
