Inicio Discusiones Geometría y medición Introducción al plano coordenado y coordenadas
Discusiones
Temas
Introducción al plano coordenado y coordenadas
Mentor: Por favor, dibujen una recta horizontal en el centro de su papel cuadriculado. A medida que contamos "Cero, uno, dos, tres,..."escribimos los números en la recta, un número en cada línea del papel cuadriculado. Cuando contamos de para atrás, diferenciamos los números que van antes de cero colocando un signo "-" al frente de ellos, así que tenemos:"dos, uno, cero...". Asegúrense de espaciar uniformemente los números puesto que la distancia de 1 a 2 debe ser la misma que hay entre 2 y 3, por ejemplo.
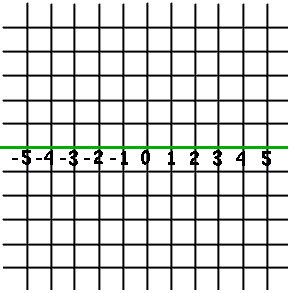
Estudiante: Menos uno, menos dos, menos tres, ...
Mentor: Así tenemos lo que se llama una "recta numérica" o "recta coordenada". Se puede usar para describir dónde está un punto de la recta. Para dar la "dirección" exacta de un punto, nos fijamos en qué tan lejos está el punto desde cero, usando un signo menos para los números que quedan a la izquierda de cero. Excepto que no lo llamamos un signo menos sino que nos referimos a estos números como "negativos".
Estudiante: Entonces la dirección de este punto (el estudiante resalta el 4) es 4, y la dirección de este punto (el estudiante resalta el -5) es 5 negativo.
Mentor: Excelente. Ahora queremos tener más libertad de movimientos. Dejaremos que nuestros puntos estén en cualquier lugar del papel, no solamente sobre la recta. Para dar la dirección de puntos que no están sobre la recta numérica necesitaremos trazar una recta numérica vertical. Dibujen una recta vertical que pase por el cero de la recta numérica horizontal. Después etiquétenla con números positivos por encima de la recta numérica horizontal y con números negativos por debajo de ella. En lugar de hablar de recta numérica horizontal o vertical todo el tiempo, usaremos sus nombres matemáticos. La recta numérica horizontal se llama el eje-x y la recta numérica vertical es el eje-y.
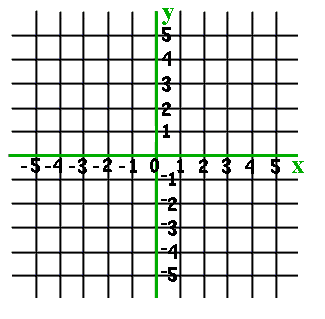
Estudiante: Bueno. Yo iria tres casillas hacia arriba y después dos hacia la derecha.
Mentor: De acuerdo. ¿De qué otra manera podrías llegar allá?
Estudiante: Podemos ir primero dos bloques a la derecha y en seguida tres bloques hacia arriba.
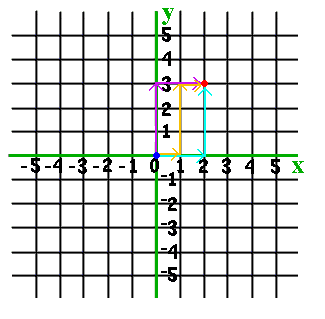
Estudiante: O podemos ir uno a la derecha, tres hacia arriba y uno más a la derecha.
Mentor: Hay muchas formas de ir de un punto a otro (a propósito, ¿cuántas formas?). Para crear una forma estándar de referirse a un punto, los matemáticos convinieron en que siempre designarían el punto según un camino especial. Arrancando de cero, recorremos todo el camino hacia la derecha o hacia la izquierda, contando pasos: uno, dos. A continuación vamos hacia arriba o hacia abajo: uno, dos, tres pasos hacia arriba. Entonces escribimos el número de pasos como (2, 3). Nuevamente, el primer número es "izquierda-derecha", el segundo "arriba-abajo". Un signo negativo significa izquierda o abajo. Así, si nuestro punto es (-2, -3), damos dos pasos a la izquierda, y enseguida tres pasos hacia abajo. ¿Recuerdas los nombres de nuestras rectas numéricas?
Estudiante: Sí, la recta horizontal se llama eje-x y la recta vertical se llama eje-y.
Mentor: ¿Puede alguien pensar en una mejor descripción de la dirección de un punto en lugar de (izquierda-derecha, arriba-abajo)?
Estudiante: ¿Podríamos designar la dirección con los nombres de las rectas?
Mentor: Si, de esta manera la dirección de un punto se describiría como (x, y) en lugar de (izquierda-derecha, arriba-abajo). El término matemático para la dirección de un punto es coordenadas. ¿Ahora todos saben cómo el eje-x y el eje-y dividen la hoja de papel en cuatro secciones?
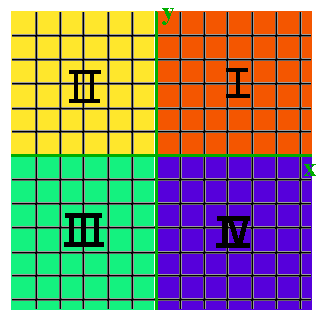
Estudiante: Sí.¡Y apuesto a que también tienen nombres!
Mentor: ¡Tienes razón! Estas regiones se llaman cuadrantes.
Estudiante:¿Se llaman cuadrantes porque son cuatro y un cuadrilátero tiene cuatro lados?
Mentor: ¡Buena observación! Nuestro prefijo "quad" se deriva de la palabra latina "quattuor" que significa cuatro. Cada uno de estos cuadrantes se designa con un númeral romano.
- El primer cuadrante contiene todos los puntos para los cuales la coordenada x es positiva y la coordenada y es positiva y se representa con el numeral romano I.
- El segundo cuadrante contiene todos los puntos con coordenada x negativa y coordenada y positiva y se representa con el numeral II.
- El tercer cuadrante contiene todos los puntos con coordenada x negativa y coordenada y negativa y se representa con el numeral III.
- El cuarto cuadrante contiene todos los puntos con coordenada x positiva y coordenada y negativa y se representa con el numeral IV.
Estudiante: ¿Todo punto que tiene una dirección (positivo, negativo) quedará en el cuarto cuadrante?
Mentor: Sí, pero usemos el vocabulario adecuado. Todo punto que tiene coordenadas (positvo, negativo) queda en el cuarto cuadrante.
Estudiante:¡Ahora podemos jugar El juego del laberinto!
