Inicio Discusiones Geometría y medición Altura inclinada
Discusiones
Temas
Altura inclinada
Estudiante: ¿Qué es la altura inclinada de un prisma triangular?
Mentor: Empecemos por observar la cara triangular en un prisma triangular.

Mentor: Las cuatro unidades cúbicas de la parte ancha del triángulo representan el ancho de la base del triángulo. La distancia desde el punto medio del ancho de la base hasta el vértice superior del triángulo es la profundidad de la base. Las longitudes de los lados del triángulo que van desde la base hasta el vértice superior del triángulo representan la altura inclinada.
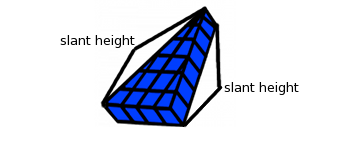 altura inclinada
altura inclinada
Estudiante: OK, entonces la altura inclinada es 6 unidades, ¿correcto?
Mentor: En realidad, no. La altura inclinada es un poco más que la profundidad de la base porque la distancia desde la esquina del lado base al vértice superior (que corresponde a la altura inclinada) es mayor que la distancia vertical desde el centro del lado base hasta el vértice superior (que corresponde a la profundidad de la base).
Estudiante: Puedo ver que es más larga, ¿qué tanto más larga?
Mentor: Bueno, tratemos de establecer qué sería la altura inclinada para este prisma triangular y tendremos la respuesta. ¿Cómo hallaríamos la longitud de uno de los lados diagonales del triángulo que representan la altura inclinada?
Estudiante: Bueno, podríamos usar el teorema de Pitágoras. Conocemos la profundidad de la base del triángulo (6), que será un cateto del triángulo. Esta línea bisecta el ancho de la base y forma un triángulo rectángulo.
Mentor: ¡Correcto! Puesto que estamos bisectando el ancho de la base, ¿cuál será la longitud de la parte que forma el triángulo rectángulo?
Estudiante: Bisectar significa dividir en dos partes iguales así que el ancho de la base (4) dividido por 2 sería 2.
Mentor: Por lo tanto el triángulo que creamos al interior de este triángulo tiene un cateto que mide 6 (ancho de la base), un cateto que mide 2 (mitad del ancho de la base) y la diagonal, que representa la altura inclinada del triángulo. ¿Qué se sigue?
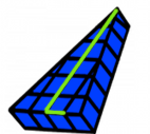
Estudiante: Bueno, podemos aplicar el teorema de Pitágoras:a 2 + b 2 = c 2
Mentor: ¿Cuál variable representa la altura inclinada?
Estudiante: La altura inclinada es c porque la hipotenusa de un triángulo rectángulo se representa siempre con la variable c, mientras que los dos catetos que forman el ángulo recta son las variables a y b.
Mentor: ¡De verdad sabes cómo usar esta ecuación! ¿Y qué haces después?
Estudiante: Remplazo los valores. Un cateto es 2 unidades y el otro es 6 unidades, entonces:
(2) 2 + (6) 2 = (c) 2
4 + 36 = c 2
40 = c 2
c= √40
Por lo tanto, c es aproximadamente 6.32 unidades.
Mentor: Wuao, acabas de calcular la altura inclinada, ¡excelente trabajo!
Estudiante: ¡Así pues, la altura inclinada en este ejemplo sería 6.32, porque esta es la longitud de cada lado que va desde el extremo de la base hasta el vértice superior!
